- トピックス
理論センターの小嶋涼太さんが第4回SOKENDAI賞を受賞
2020年4月9日
-

長谷川学長(写真中央)から贈られた賞状を手に微笑む小嶋涼太さん(写真右)。 / ©️総合研究大学院大学
KEK理論センターの協力研究員である小嶋涼太さん(当時の所属は総合研究大学院大学(総研大) 高エネルギー加速器科学研究科 素粒子原子核専攻)が第4回SOKENDAI賞を受賞し、2020年3月25日に授賞式が執り行われました。
SOKENDAI賞は、総研大の理念と目的に照らして、特段に顕彰するに相応しい研究活動を行い、その成果を優れた学位論文にまとめて課程を修了し、学位を取得した修了生を表彰する賞として平成30年度に創設されました(引用 総合研究大学院大学webサイト)。
小嶋さんが受賞した学位論文のタイトルは「Triangulation of the Amplituhedron from Sign Flips(日本語名:符号反転を用いた散乱多面体の三角分割)」です。小嶋さんは素粒子理論の研究をしており、特に「散乱振幅」という物理量に注目していました。素粒子の種類や振る舞いには未だ謎が多く、現在素粒子物理学の大きな謎の一つとして、世界中で加速器を用いた実験研究が進められています。ところが、実験データと比較しつつ理論から素粒子の振る舞いや種類を導くためには、散乱振幅を用いた計算が必要になります。
これまでの理論研究で、散乱振幅がある種の多面体の体積として計算できることが分かっていました。ですが、なぜ振幅と多面体に繋がりがあるのか、多面体の形が高次元で複雑な場合に振幅からどのように多面体の体積を計算するのかといった未解明な点が多く残っていました。そこで小嶋さんは散乱振幅からどのように振幅多面体が得られるか調べるため、「三角分割」という方法を用いました。三角分割とは、多面体をより低次元の形に分割して考える方法です。
-
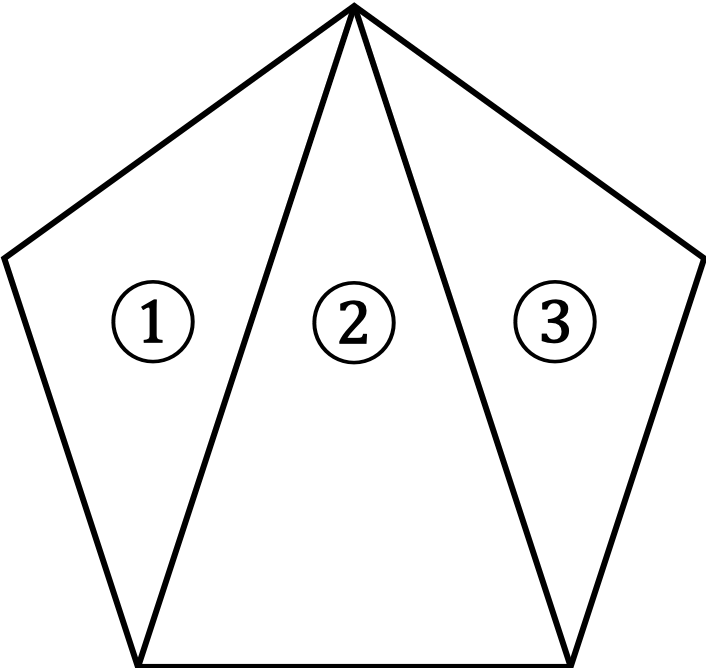
簡単のために二次元で考えると、例えば五角形の面積を考える際、五角形を3つの三角形①、②、③に分割してそれぞれの面積を足し合わせて求めると、五角形単体で考えるより単純な計算で面積を求めることができます。これが三角分割法です。ここでは二次元で考えましたが、小嶋さんの研究ではさらに高次元で考えます。
この三角分割法自体は昔から使われている手法ではあるものの、今回考えている多面体は一番単純なものでも五次元で、我々の住んでいる三次元の世界では高次元の多面体を視覚的に調べることができず、それを用いてどのように高次元の多面体を分割するか調べるのは難解でした。ですが、小嶋さんはこの方法で高次元の多面体の体積を計算可能にしました。
受賞した小嶋さんにお話を伺いました。
―受賞した感想を聞かせてください。
●小嶋さん SOKENDAI賞をいただけて非常に光栄です。博士論文の研究ができたのは、指導教員の北澤良久 教授(理論センター)と、アメリカに4ヶ月滞在した際に現地で振幅多面体について教えて下さった教員のおかげです。アメリカには総研大のインターンシップで行くことができました。皆様に感謝しています。
―今回の研究で一番難しかった点や苦労した点は?
●小嶋さん 振幅多面体の研究をしている研究者が日本にはいなかった点です。物理の議論は周囲の人とすぐにできましたが、振幅多面体に関してはアメリカの研究者と議論することも多く、大変でした。
―時差もあり大変でしたでしょうが、日本では小嶋さんが振幅多面体の第一人者ということですね。それでは最後に今後の目標を教えてください。
●小嶋さん これまで取り組んできた研究をさらに突き詰めたいです。現在は、理論で仮定されている世界でしか振幅多面体は見つかっていません。つまり、この理論では現実世界の素粒子を記述していないので、直接の実験結果と理論を比較することができません。ですので、今後は現実の素粒子を記述している振幅多面体の理論を見つけたいです。さらには、なぜ散乱振幅が多面体の体積として計算できるのか、記述できる根本にはどのような原理があるのか調べたいです。そして世界の様々な研究者に注目していただけるような研究成果を出せたらと考えています。
―ありがとうございました。











