グラフェンとディラックの海

ハイライト

グラフェンとディラックの海

2010年11月18日

図１

２次元物質グラフェン。白と黒で表された２つの炭素原子を基本単位として２次元に連なっている。

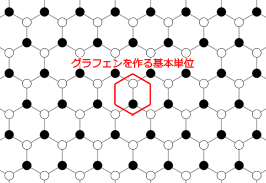
2010年のノーベル物理学賞は、英マンチェスター大のアンドレ・ガイム、コンスタンチン・ノボセロフの両博士に贈られました。その授賞理由は「２次元物質グラフェン(図1)に関する革新的実験」。グラフェン中の電子は、障害物があってもそれをすり抜けて高速度で移動します。その結果、電流を導くグラフェン電子の移動速度は、室温のシリコンのような通常の半導体の10 倍～100 倍以上となります。このためグラフェンによるトランジスタは、100GHzの領域を超えて、シリコン（Si）によるトランジスタでは到達不可能とされるテラヘルツ（THz）領域の動作が実現できると期待されています。この際立った特性は、高速で運動する電子の理論に登場する「ディラックの海」により説明することができます。

ディラックの海

イギリスの理論物理学者P.A.ディラック博士は、1928年、相対論的量子力学の式、「ディラック方程式」に関する論文を発表しました。それまでのオーストリアの理論物理学者シュレディンガーの方程式は波動の空間における位置の情報と、時間の情報の扱いが異なっていたため、空間と時間を同等に扱うことができず、アインシュタインの相対性原理を満たしていなかったのです。相対性原理を満たすように作られたディラックの方程式は、高速で移動する電子の運動を予測する方程式となることができ、４つの式から成る連立方程式で表されています。

当時、実験から電子はスピンという角運動量を持ち、その大きさが決まっていて、ただその方向だけが変わりうるような自転現象と考えられもしました。しかし、大きさを持たない電子の自転は不合理なため、ドイツの理論物理学者パウリは一個の電子に対し、２成分の波動関数を導入。上向き状態を表す第１成分と下向き状態を表す第２成分を重ね合わせることで、任意の向きの状態が作られるとし、自転という概念からスピンを解放しました。パウリの電子の方程式は２つの式から成る連立方程式でした。

ディラックの方程式はその倍の４つの式で１個の電子の状態を表します。電子が低速で運動する場合には、ディラックの４つの式のうち２つの式がパウリの方程式になります。残りの２つの式は電子が負のエネルギーを持つ場合の２つのスピン状態を表します。

相対性原理のために、電子は負のエネルギー状態をとれるという奇妙なことになってしまいました。正エネルギーの電子は光を出して負のエネルギー状態に落ち込んでしまい、無限に低いエネルギーへ移ってしまいます。これを回避するために、1930年、ディラックは真空に対して次の仮定をしました：通常は全ての負のエネルギー状態には完全に電子が詰まっている（ディラックの海）と。

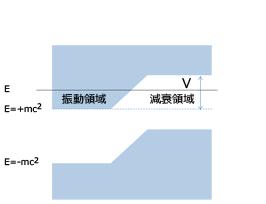
図２上

ディラックによれば電子はそのエネルギー（E）として、電子の質量をｍ、光速度をｃとしたとき、mc²以上の正のエネルギー状態と、-mc²以下の負のエネルギー状態になることが可能。しかし、負のエネルギー状態には既に電子が詰まっている（ディラックの海）ために、電子が負のエネルギーに無限に落ち込むことはないとした。

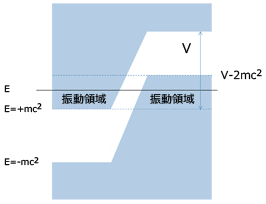
図２下

負エネルギーの電子に２倍のmc²以上のエネルギーの光があたると、そのエネルギーを受けて、正エネルギーの電子になる。元の負のエネルギー電子の跡には穴があき、これが陽電子となる（電子と陽電子の対生成）。また、正エネルギー電子が光のエネルギーを放出して、穴である陽電子に落ち込むと、電子と陽電子が消える（対消滅）。

この仮定から、陽電子の存在が予測されます。負エネルギー状態にある電子にエネルギーが与えられ、正のエネルギーになると、その真空に穴があきます。その穴は負のエネルギーが空いたので、正のエネルギーを持ち、しかもその穴は負の電荷を持った電子の空いた状態なので、正の電荷を持った穴となります。この正の電荷を持った正のエネルギーの穴が陽電子です。もちろん当初はこの奇妙な仮説を真面目に受け取る人はいませんでした。しかし、1932年、米国の実験物理学者C.D.アンダーソン博士が宇宙線の軌跡を霧箱で観測中に陽電子を発見し、この仮説の有効性が認識されました。

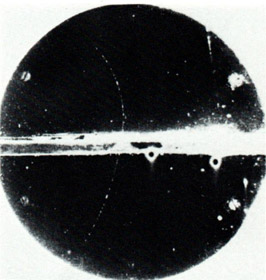
画像提供：バークレイ研究所

図３

アンダーソン博士が霧箱で観測した陽電子の軌跡。アンダーソン博士は記録された粒子の運動の向きを特定するために、鉛の板を挿入した。板を通過した粒子は運動量を失うので磁場中にあれば、軌跡の曲がり方が大きくなる。写真では、下から上に粒子が抜けたことがわかり、軌跡の曲がり方と磁場の関係からこの粒子が正の電荷を持つことが判明した。また、イオン化によって形成された飛跡が非常に細いことから、質量の小さい粒子であることもわかる。

相対論的電子のトンネル効果

ここで、エネルギーEを持つ電子が自由空間を飛んでいることを考えます。その電子がV＞Eというエネルギーを持つ壁のところにやってきました。エネルギーの壁とは壁の堅さに対応します。Vを越えるエネルギーを持っていないので、堅い壁で電子は跳ね返されてしまいます。これは、ニュートンの時代の電子の運動の考えです。ところが、シュレディンガーの方程式によれば電子は波動という性質をもつためにエネルギーが足りなくても、堅い壁の中に、ごく稀に入っていくことができます（図４）。これが「トンネル効果」です。堅い壁になればなるほど、跳ね返されやすいのでトンネル効果もおこりにくくなることが予測されます。ところが逆にディラックの方程式では、もっとエネルギーの高い壁、とても堅い壁に直面すると、壁を通過しやすくなることが予想されました（図５）。エネルギーの高い壁の領域が粒子を斥けるという常識は、エネルギーの高さVが電子の静止質量の２倍を越えると破たんする、と1929年に指摘したのがスウェーデンの理論物理学者クライン博士です。そこで、この現象をクラインのトンネル効果と呼びます。但し、実際には電子の静止質量エネルギーの２倍を越える高エネルギーの堅い壁を作らないといけないので、クラインのトンネル現象を起こすのは容易ではありません。

図４

自由空間を運動していたエネルギーEの電子がエネルギーV＞Eの壁に到達したときの概念図。ニュートン力学では図中の白い領域は禁止領域なので入っていけず、跳ね返されてしまう。しかし、シュレディンガーの方程式によると、電子は波動なので、エネルギーの高いＶの領域にも入っていける。これをトンネル効果という。但し、壁の外の自由空間では波動は振動的だが、Vの壁の中では著しく波動が減衰する。

図５

エネルギーＥの電子が、より高いエネルギーVの壁に直面すれば、さらに強く減衰すると思わる。しかし、ディラックによれば、エネルギーVがV-E>mc²より高くなると、電子の波動は振動的になり壁に入っていく。これをクラインのトンネル効果と呼ぶ。

グラフェンでおきるトンネル効果

それでは、グラフェンでは何がおこるのでしょうか。そもそもグラフェンとは、炭素の結合状態で最も安定とされているグラファイトで、炭素原子がハチの巣格子状に共有結合した平面のシートの一枚一枚のことでした。炭素の４つの価電子のうちの３つが隣接する原子との結合に使われ、残りの１つが自由電子のように自由に動き回れる電子（パイ電子）としてグラフェン上を運動します。その移動速度は、常温で光速の300分の１と言われています。また、図１の白と黒の点で表されているように、グラフェンは２つの炭素原子を基本とする組み合わせと考えることができ、このためグラフェンのパイ電子も２成分を持ちます。この２成分はスピンの２成分のアナロジーで、擬スピンと呼ばれます。擬スピンの存在からグラフェンのパイ電子もディラック方程式に従って運動することになります。しかもグラフェン中ではパイ電子はその質量が零のように運動することが分かっているので、静止質量の2倍の高いエネルギーの壁の設定の必要がなく、クラインのトンネル効果が起きるのです。こうしたグラフェンのトンネル効果を応用した今までより10倍から100倍速く計算できる計算機の実現が期待されています。

ハイライト