- トピックス
【研究者向け】深層学習によるパラメータ空間スキャン手法を提案
2025年8月6日
多くの変数がある現象で、条件を満たす最適な点を探す変数スキャンは、しばしば膨大な計算時間を要します。KEK素粒子原子核研究所の研究員であるAhamed Hammad 氏 (学術変革領域研究「学習物理学」研究員)と、Korea Institute for Advanced Study (KIAS) Quantum Universe Center研究員のRaymundo Ramon 氏は、深層学習とVEGAS法と呼ばれる数値積分手法を組み合わせ、このスキャンプロセスを加速するプログラム「 DLScanner 」を公開しました。この手法は、多数の自由変数をもち、計算コストの高いあらゆる問題に対して効果的であると期待されています。
-
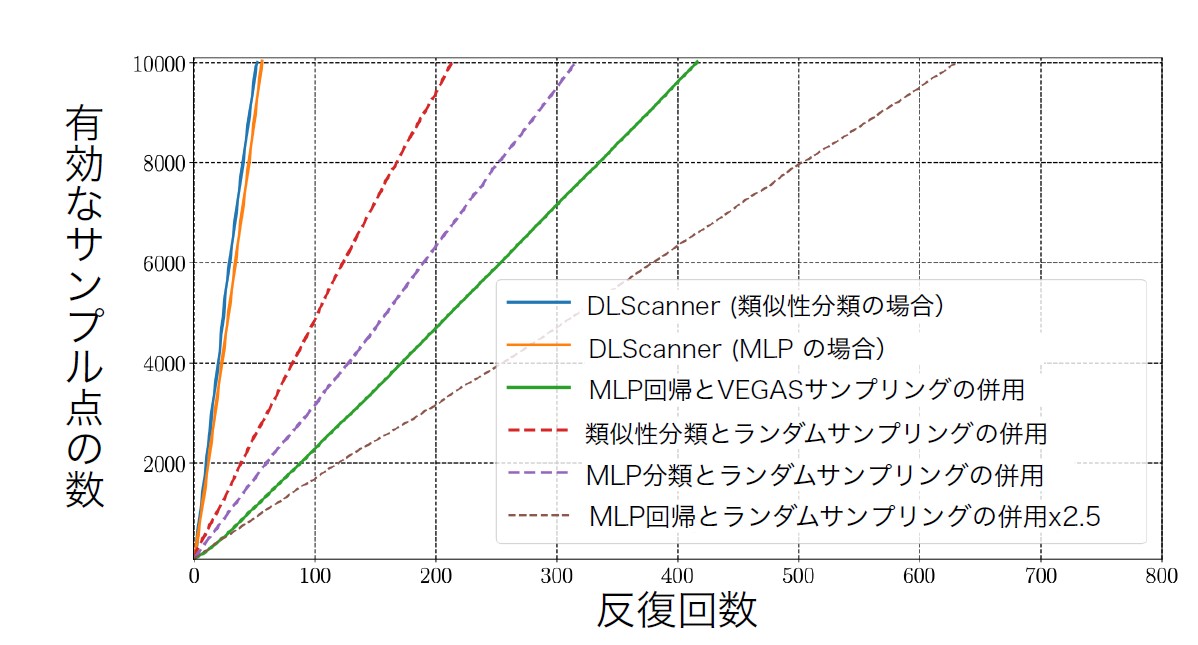
本研究で提案するDLScanner (VEGASサンプリングと深層学習分類器の併用による、変数探索)とランダムサンプリングによる変数探索の比較。アルゴリズムの反復回数(横軸)を増やすにつれて、変数スキャンに有効なサンプル点の数(縦軸)は増えるが、DLScanner (青または、オレンジの実線)はランダムサンプリングや回帰分析によるアルゴリズムに比べ、少ない反復回数で有効サンプルを収集している。
本論文で革新的な点
高次元変数空間の中で、複雑な条件を満たす点の探索(変数スキャン)は、計算資源を大きく消費し、非常に時間がかかります。深層学習を活用して、このプロセスの効率化を図ることは可能でしょうか?ニューラルネットワークは、サンプリング空間から目的とする領域への複雑で高次元な写像を学習できます。一度訓練されると、所定の制約を満たす可能性が高い変数を高速で予測することが可能になります。この技術により、1点ごとの評価に高い計算コストが必要な場合でも、高次元空間の変数スキャンが大幅に加速されます。
概要
これまでに、複雑な変数空間を探索(スキャン)するため、様々な戦略が提案されてきました。最も単純な方法としては、格子状に区切った空間の点に限った計算を行う「グリッドサンプリング」やランダムな点の上で計算を行う「ランダムサンプリング」があります。これらの手法は空間全体を網羅的にスキャンできる一方で、興味のある領域への収束が遅いため、実用上は非効率です。これに対し適応的サンプリング手法では反復的に尤度関数を最適化することによって、目的とする領域にスキャンを集中させることができます。このような手法の例としてはMCMC やMultiNest が知られています。しかし、鋭い特徴や不規則な構造を持つ変数空間では、評価回数が増えたり、十分にスキャンできない場合があります。
Ahamed Hammad氏とRaymundo Ramon 氏 はニューラルネットワーク(NN) を使った新しい適応的サンプリング手法を用いるDLScanner を公開しました。DLScanner は変数空間のスキャンに対して、柔軟で強力な代替手段を提供します。深層学習モデルを反復的に訓練し、制約を満たす可能性が高い候補点を予測することで、計算負荷の大きい設定でも効率的なスキャンが可能になります。
手法
本研究で提案するスキャン手法は、次の2つの主要な構成要素から成ります。
-
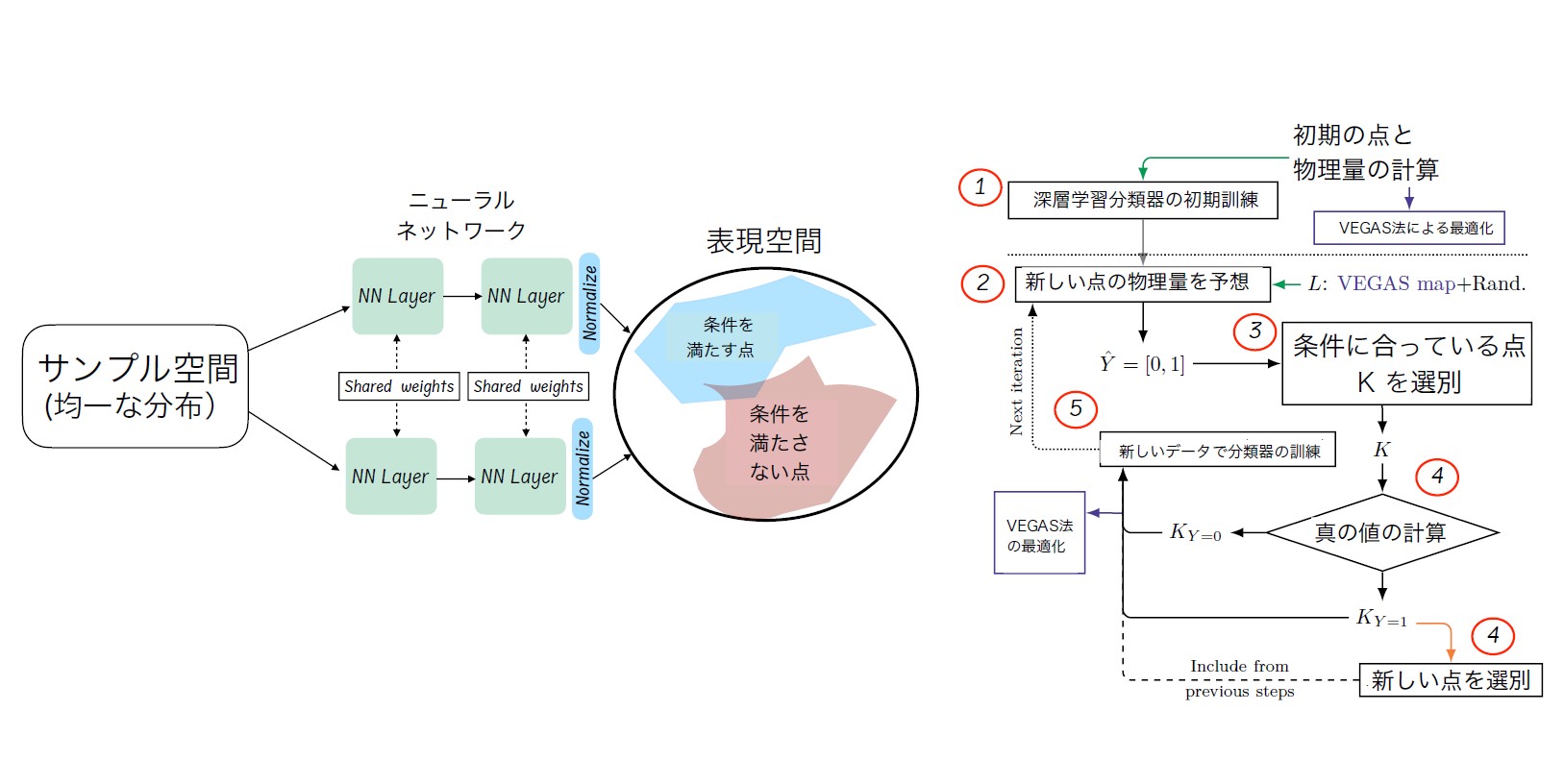
左)類似性学習ネットワークの構造 右)DLScanner の全体構造
類似性学習ネットワーク
サンプリングされた点を潜在的な表現空間に射影するNNです。この空間では、制約を満たす点は互いに近く配置され、満たさない点は遠ざけられるように、構成されます(図1左)。このように構成することで、NNは潜在空間の幾何学を理解し、目的とする適応的サンプリングへ早く収束して、条件を満たす点を早く生成できるようになります。具体的にはネットワークは対照損失(Contrastive loss)関数を最小化し、表現空間を超球面上に構築することです。これにより、有効・無効な点の間のユークリッド距離が最大化しています。
動的サンプリング
有効領域に対して高密度なサンプルを生成するために、VEGAS法をスキャンループに統合しました。 従来は多次元積分で使われていたVEGAS法を再設計し、サンプル点の分布が動的に最適化されるようにしています。これにより、有効領域において密度が高くなるように新しい点が生成され、収束がさらに加速されます。例として、2次元空間上のドーナツ型関数
F2d (x1, x2)= [2 + cos(x₁)⁵·cos(x₂)⁷]⁵
に対して F2d = 100 ± 5 を満たす点を見つけるアニメーションを、以下のリポジトリに掲載しました。
https://gitlab.com/Ahammad115566/dlscanner/-/blob/main/2d.mov?ref_type=heads
変数スキャン手順
図1右 に示したステップを段階的にとります。図の数字は以下のステップを表しています。
- 初期化:ランダムな変数を用いて、最初のネットワーク訓練用データを生成します。
- 予測:ニューラルネットワークにより、多数のランダム点の出力を予測します。
- 選択:予測結果に基づき、有望な点を選定します。
- 評価・修正:選定された点の真の値を評価し、ネットワークの予測と比較します。特に、両者が十分に一致する点を追加することでデータを精緻化します。
- 再学習:蓄積されたデータセットを用いて、ネットワークとVEGASを再訓練します。
- 反復:以上のステップを繰り返しながら新しい点を生成し、ネットワークとVEGASの訓練を再帰的に行います。
応用例
提案手法は、制約条件の下で高次元の自由変数をスキャンする必要がある多くの分野に適用可能です。例えば、本論文では、素粒子物理学において重要な2つのヒッグス2重項のある模型(2HDM)のヒッグスポテンシャルの質量変数と結合定数のスキャンにDLScanner を応用しています。このポテンシャルの質量変数や結合定数を、理論的・実験的制約を満たすように決定することが課題です。
これらの変数の各点における理論的予言には、理論的にも実験的にもさまざまな制限がかかりますが、著者の計算環境ではこの理論的予言を計算するのに1点あたり9秒かかります。それぞれの変数のステップをn 自由度の数をd とした場合、グリッドスキャンするために必要な計算量は9x nd となり、精密な計算をするためにnを増やすと、爆発的に増大します。一方、MCMCを用いた場合は、1ステップあたり100点の計算を行うと、140 回の再帰的計算で収束し、全体として、1.3×105秒かかります。これに対し、DLScanner は75回の再帰的計算で収束し、6.8×104秒で同等の成果を達成します。さらに、DLScanner はMCMCでは対応できない、40変数の模型の変数スキャンも行うことができます。
掲載論文
タイトル:DLScanner: A parameter space scanner package assisted by deep learning methods
著者:A. Hammad and Raymundo Ramos
arXiv:2412.19675 [hep-ph]
掲載誌:Computer Physics Communications, Vol. 314 (2025), 109659
公開コード
PyPIパッケージ:
https://pypi.org/project/DLScanner/
インストールコマンド:
pip install DLScanner==1.0.0











