新粒子を組み立てる公式

2012年07月13日 #ハイライト

KEKからも多くの研究者が参加し、スイス・ジュネーブにある欧州合同原子核研究機関(CERN)で研究を行っている、ATLAS(アトラス)実験グループは、2012年7月4日に、ヒッグス探索の新しい結果を発表しました(関連記事)。それによると、質量126GeV/c²付近に新粒子を観測し、その性質は標準理論^※で唯一確認されていないヒッグス粒子とも合っているようです。今回のハイライトでは、このアトラス実験グループからの発表をもとに、新しい素粒子の探し方を解説します。

ヒッグス粒子はLHC加速器で作られたとしても、ほとんど瞬間的に他の安定した粒子に変化(崩壊)してしまうので、研究者はその変化してしまった粒子から、もともとの粒子を組み立てなおすことを行います。その組み立て直すのに使われる公式は、アインシュタイン博士の有名な式、E=mc²に関係があります。Eはエネルギー、mは粒子の質量、cは光の速度、秒速30万キロメートルです。

しかし、この式は粒子が止まっている時の式で、粒子が動いているときのより一般的な公式は、
つまり、E²−P²c²＝m²c⁴となります。Pは運動している粒子の運動量。運動量は粒子が遅く運動している時には、質量と運動の速度をかけた量で、その運動している粒子の「勢い」とその向きを表します。P²と書いたときは、その大きさの二乗です。加速器実験では、粒子が測定器の中を通過する時に、磁石によって曲げられた飛跡の曲がり具合から測定できます。粒子が止まっているときは、運動量が0(P＝0)なので、この式は、E²＝m²c⁴、つまり、E=mc²の両辺を二乗した式になります。

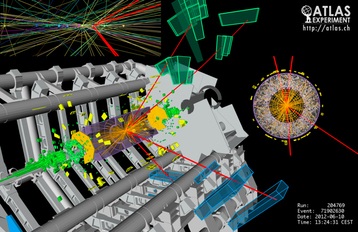
図1：ヒッグス粒子が4つのミューオンに崩壊する事象の候補(2012年ATLASデータ)。図1は、ATLAS測定器が記録した、陽子と陽子が衝突して2つのミューオンと2つの反ミューオンが現れた反応です。親となる新粒子からこれら4つの粒子が作られたと仮定すると、その親の質量を、この公式を使って計算することができます。

測定された4つの粒子のエネルギーをそれぞれ、

ミューオン1のエネルギーがE₁、
ミューオン2のエネルギーがE₂、
反ミューオン3のエネルギーがE₃、
反ミューオン4のエネルギーがE₄、

とします。一方、運動量は向きを持った量なので、x軸、y軸、z軸のそれぞれの方向に測定でき、

ミューオン1の運動量がP_1x、P_1y、P_1z、
ミューオン2の運動量がP_2x、P_2y、P_2z、
反ミューオン3の運動量がP_3x,、P_3y、P_3z、
反ミューオン4の運動量がP_4x、P_4y、P_4z、

であったとします。親粒子から4つの粒子ができたので、もともとの親粒子のエネルギーEは、E₁+E₂+E₃+E₄であったはずです。また、運動量もそれぞれの3次元の軸毎に足して、親粒子の運動量は

x軸方向に、P_x＝P_1x+P_2x+P_3x+P_4x_、
y軸方向に、P_y＝P_1y+P_2y+P_3y+P_4y、
z軸方向に、P_z＝P_1z+P_2z+P_3z+P_4z、

であったはずです。親粒子の運動量Pの二乗は、それぞれの成分Px、Py、Pzを二乗して足せばよいので、P²＝P_x²＋P_y²＋P_z²。ここで公式を使えば、親粒子の質量の二乗が、M²=(E²-P²c²)/c⁴として計算できます。

ミューオン1にも公式が使えます。ミューオン1のエネルギーはE₁、運動量は、P₁²=P_1x²+P_1y²+P_1z²なので、公式を使えば、E₁²-P₁²c²=m²c⁴。ミューオンの質量mは0.1GeV/c²と小さいので、E₁²とP₁²c²はとても近い大きさを持っています。他のミューオンでもエネルギーと運動量×cはほとんど同じ大きさです。ところが親粒子の運動量は、例えばx軸方向の量、P_x＝P_1x+P_2x+P_3x+P_4xを計算する時に、反対向きに飛んでいく4つの粒子の運動量を足し合わせるために、打ち消し合って、小さくなります。同じことが、y軸、z軸方向の親粒子の運動量P_y、P_zにもおきるので、親粒子の運動量P²＝P_x²＋P_y²＋P_z²は、エネルギーEに比べて小さくなることができ、それで、Mが大きい場合があっても良いということになります。

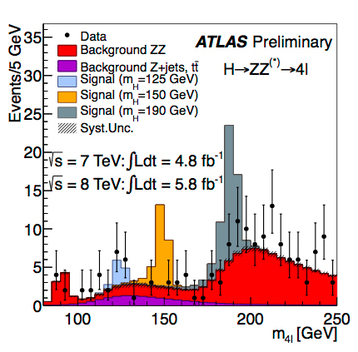
図2：4つのレプトンがひとつの親粒子から変化したと仮定した時の質量分布。以上が測定の原理ですが、実際の実験では色々な技術的な問題に出会います。たとえば、粒子のエネルギーE₁やP₁といった測定値にはどれほど信頼がおけるでしょうか。4つの粒子の運動量とエネルギーを組み合わせる、といっても、その4つの粒子が同じ1つの粒子の崩壊で生まれたのでなければ、上の計算が与える結果は意味のないものになります。データを正しく理解するには、測定器の精度を詳細にチェックしたり、得られた結果を統計的に解釈したりするなどのことが必要になります。実験グループのメンバーは、こうした問題を隅々まで確認してから初めて、国際会議や学術雑誌で結果を発表します。学会での議論も、こうしたチェックがどのくらい綿密に行われているかに多くの時間が費やされます。

図2はそうした解析の実例です。黒丸は、ATLAS測定器が測定した2つのミューオンと2つの反ミューオンから組み直したときの親質量Mの分布を示します。黒丸についている棒のようなものは、統計誤差の大きさを示す誤差棒(エラーバー)です。ここでは、電子と陽電子とミューオンと反ミューオンの4つが一度に観測された場合、2つの電子と2つの陽電子が観測された場合の両方を足しあわせてプロットしています。標準理論が正しいと仮定すると、ヒッグス粒子が弱い力を媒介する2つのZ⁰ボソンに変化し、その2つのZ⁰ボソンのそれぞれが、更にミューオンと反ミューオン、または、電子と陽電子に変化することを予測することができます。電子やミューオンは合わせてレプトンと呼ばれるので、「4レプトン反応の解析」と呼ばれます。

赤いヒストグラムは、標準理論のまま、ただし新粒子が存在しないとしたとき、4レプトン反応がどんな分布をするか、予測したものです。ヒストグラムは計算シミュレーションによるもので、実測ではありません。この場合、ほとんどの4つの粒子は、ある粒子から作られるわけではないので幅広く分布します。しかし、赤いヒストグラムの左端のところではちょっとした盛り上がりが見られます。これは陽子と陽子が衝突して、Z⁰粒子が1個作られ、それが4つの粒子に変化した場合であることを示します。Z⁰粒子は質量が約91GeV/c²なので、そこにZ⁰粒子1個が作られ、それを介しての4レプトンという反応が記録されたわけです。実測データ(黒丸)でも、盛り上がりのようなものが見えているのが分かります。

一方、水色、橙色、灰色のヒストグラムは、標準理論で予言するヒッグス粒子が存在すると仮定して、その質量がそれぞれ、125GeV/c²、150GeV/c²、190GeV/c²であった場合、4レプトン反応がどんな風に見えるかを予測したものです。これも計算シミュレーションで、実測ではありません。橙色や灰色のヒストグラムは黒丸の実測データと合っていません。ですが、水色のヒストグラムなら実験データが示す125GeV/c²付近の盛り上がりをよく説明しているように見えます。

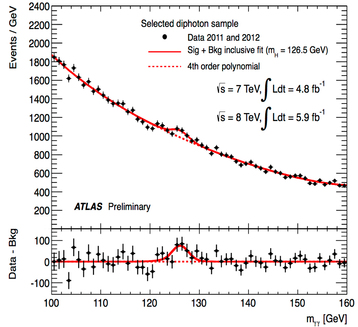
図3：2光子反応における質量分布。また、図3はATLAS測定器による2つの光子を観測した反応を使い、2つの光子のエネルギーや運動量から、同じように2つの光子がひとつの粒子から作られたと仮定した時の親粒子の質量をプロットしたものです。

この図でも実験データは黒丸の点で表されています。一方赤線は、126.5GeV/c²に盛り上がりをつくるという条件をつけて、黒丸のデータ点をもっともよく再現できる式を探した結果です。標準理論は、1つのヒッグス粒子がある質量を持っている時に2つの光子に変化する割合を予測します。赤線の盛り上がりは標準理論の予測の1.9倍±0.5倍で、誤差の範囲でよく一致しています。

このように、ATLAS実験グループは、4レプトン反応と2光子反応の両方の解析から約126GeV/c²の質量を持つ新粒子を観測し、また、それが標準理論のヒッグス粒子であると仮定した時の予測が、それらの分布をよく説明できることを示しました。そして、"つぎの数週間、数ヶ月の間にATLASはこれらの性質をより良く測定し、これらの事象が果たしてヒッグス粒子によるものなのか、それとも複数のヒッグス粒子ファミリーの中で最初に発見された粒子なのか、あるいは全く新しい何者かであるのか、これらの問いに関してより明確な解釈ができるように努める"としています。

用語解説

※　標準理論
素粒子とその間にはたらく3つの力(強い力、弱い力、電磁気力)を記述する理論の枠組み。現在最も適切に物理現象を説明できる理論体系であり、標準模型、標準モデルとも呼ばれる。

新粒子を組み立てる公式

関連サイト

関連記事