超伝導状態を理解する上で重要な物理量としてコヒーレンス長(ξ
0)と呼ばれる長さがあります。これは超伝導を担う電子対(=Cooper対)において、電子がお互いに対の相手として認めあう距離(相関距離)を意味し、フェルミ面上での電子の速度VFに比例する一方で超伝導ギャップΔ
0に反比例します(ξ
0~
hv/Δ
0)。よく知られているように、第二種超伝導体の特徴はこのコヒーレンス長がもう一つの基本的な長さである磁場侵入長λよりずっと短い(ξ
0<<λ)、という点にあります。この場合、磁場中で金属全体の超伝導状態を破壊してしまうよりも、磁束量子(φ
0=2.07×10
9G/A2)と呼ばれる量子化された磁束が超伝導体を貫通し、その部分のみで超伝導が壊れた状態の方が安定(=自由エネルギー
*が小さい)になります。これを磁束格子状態、あるいは混合状態と呼びます。
ちなみに超伝導状態の本質は、対になった電子の波動関数(基本的に平面波∝exp(
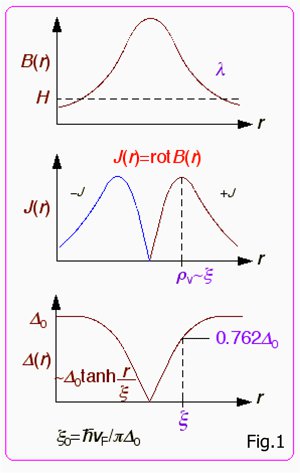
ikr)に比例)の空間位相が超伝導体のどの位置でもゼロになっている(krと-krが打ち消し合う)という点にあり、磁束量子はちょうどその磁束による波動関数の位相変化が2πとなってゼロと等価になるために超伝導状態と共存できるのです。また、これらの磁束は、空間的な平均の磁場が外部磁場とほぼ一致するような格子間隔で並び、格子の形も通常は三角格子であることが知られています。さて、それでは磁束一本一本を眺めたとき、超伝導はどの程度の領域で壊れているのでしょうか。図1にあるように、実は厳密に言うと超伝導ギャップがゼロになっているのは磁束の中心点(=特異点)だけで、そこから遠ざかるにつれて超伝導は徐々に回復し、ある特徴的長さξよりずっと遠方で本来の値Δ
0に戻ります。このギャップの空間的な不均一さの度合いを特徴づける長さをGinsburg-Landauのコヒーレンス長と呼びます。これは初めに出てきた長さξ
0と低温・高磁場の極限では一致すると考えられていますが、基本的には与えられた温度・磁場で自由エネルギーが最小になるように変化する量です。 磁場の上昇とともに磁束格子の間隔が狭まり、最終的にξより狭くなったとすると超伝導が壊れた方がエネルギー的に得になるので、この時上部臨界磁場Hc2からξの極限値ξ
GLがH
c2=φ
0/2πξ
GL2という関係で導かれます。
それではξ(
T,H)は有限の温度・磁場でどのように変化するのでしょうか。これは現在でも未解明の部分が あるテーマの一つで、混合状態をより深く理解するために実験・理論双方から様々な研究が行われています。 まず、温度の効果として、低温ほど顕著になると予想される効果にKramer-Pesch効果というものがあります。 これは磁束付近の超伝導ギャップに図1のような空間変化があることから、Cooper対を形成していない電子 (=常伝導状態にある電子、ギャップを超えた励起子という意味で準粒子とも呼ばれる)が磁束コア付近に 離散的な束縛状態を作ることによるもので、温度のエネルギースケールがこの束縛状態の準位間隔より小さく なると低い準位のみが占有され、ξが実効的に縮むと予想されています。次に磁場の効果ですが、これは主な ものだけでもZeeman効果による直接的なCooper対の破壊に加えて、上記準粒子が磁束を周回する超伝導電流に 流される効果(Dopplerシフト)、狭くなった磁束の間を飛び移る効果(磁束格子効果)、隣接する磁束間で 超伝導電流が部分的に打ち消し合う効果、等が考えられます。ただし、これらの磁場効果は高磁場ほど顕著に なるもので、通常の超伝導体の場合、低磁場では無視できるものです。
さて、我々のグループでは、磁束状 態の磁場分布から磁束の構造を微視的に観察できるμSR法を用いてこれらの問題を研究していますが、 最近代表的な銅酸化物超伝導体の一つであるLa
2-xSr
xCuO
4(LSCO)の低磁場中において奇妙な現象を観測したので、それについてご紹介しましょう。
「最近の研究から?YNi
2B
2Cの磁束状態」の節でも紹介されているように、μSR法を用いると磁束格子状態 の空間的な磁場分布
B(r)について、その平均を密度関数
n(
B)の形で得ることができます。 この
n(
B)と磁束格子の形の情報を用いると磁場分布
B(
r)を再構成することができます。 図2 がそのようにして再現されたYNi
2B
2Cの磁束格子状態における磁場分布です。この例では格子が四角格子になっ ていることが中性子小角散乱等の実験から明らかになっており、その原因としてフェルミ面の異方性のために 超伝導電流が「四角」に流れている(V
Fが[100]方向と[110]方向で大きく異なる)ことによると考えられてい ます。図2はそのような効果をも考慮して再構成されたものですが、実際に一本一本の磁束の周りの磁場分布 が強い四回対称性を持っており、全体として電磁エネルギーを下げるために四角格子を組んでいる様子が分かります。
 超伝導状態を理解する上で重要な物理量としてコヒーレンス長(ξ0)と呼ばれる長さがあります。これは超伝導を担う電子対(=Cooper対)において、電子がお互いに対の相手として認めあう距離(相関距離)を意味し、フェルミ面上での電子の速度VFに比例する一方で超伝導ギャップΔ0に反比例します(ξ0~hv/Δ0)。よく知られているように、第二種超伝導体の特徴はこのコヒーレンス長がもう一つの基本的な長さである磁場侵入長λよりずっと短い(ξ0<<λ)、という点にあります。この場合、磁場中で金属全体の超伝導状態を破壊してしまうよりも、磁束量子(φ0=2.07×109G/A2)と呼ばれる量子化された磁束が超伝導体を貫通し、その部分のみで超伝導が壊れた状態の方が安定(=自由エネルギー*が小さい)になります。これを磁束格子状態、あるいは混合状態と呼びます。
ちなみに超伝導状態の本質は、対になった電子の波動関数(基本的に平面波∝exp(ikr)に比例)の空間位相が超伝導体のどの位置でもゼロになっている(krと-krが打ち消し合う)という点にあり、磁束量子はちょうどその磁束による波動関数の位相変化が2πとなってゼロと等価になるために超伝導状態と共存できるのです。また、これらの磁束は、空間的な平均の磁場が外部磁場とほぼ一致するような格子間隔で並び、格子の形も通常は三角格子であることが知られています。さて、それでは磁束一本一本を眺めたとき、超伝導はどの程度の領域で壊れているのでしょうか。図1にあるように、実は厳密に言うと超伝導ギャップがゼロになっているのは磁束の中心点(=特異点)だけで、そこから遠ざかるにつれて超伝導は徐々に回復し、ある特徴的長さξよりずっと遠方で本来の値Δ0に戻ります。このギャップの空間的な不均一さの度合いを特徴づける長さをGinsburg-Landauのコヒーレンス長と呼びます。これは初めに出てきた長さξ0と低温・高磁場の極限では一致すると考えられていますが、基本的には与えられた温度・磁場で自由エネルギーが最小になるように変化する量です。 磁場の上昇とともに磁束格子の間隔が狭まり、最終的にξより狭くなったとすると超伝導が壊れた方がエネルギー的に得になるので、この時上部臨界磁場Hc2からξの極限値ξGLがHc2=φ0/2πξGL2という関係で導かれます。
それではξ(T,H)は有限の温度・磁場でどのように変化するのでしょうか。これは現在でも未解明の部分が あるテーマの一つで、混合状態をより深く理解するために実験・理論双方から様々な研究が行われています。 まず、温度の効果として、低温ほど顕著になると予想される効果にKramer-Pesch効果というものがあります。 これは磁束付近の超伝導ギャップに図1のような空間変化があることから、Cooper対を形成していない電子 (=常伝導状態にある電子、ギャップを超えた励起子という意味で準粒子とも呼ばれる)が磁束コア付近に 離散的な束縛状態を作ることによるもので、温度のエネルギースケールがこの束縛状態の準位間隔より小さく なると低い準位のみが占有され、ξが実効的に縮むと予想されています。次に磁場の効果ですが、これは主な ものだけでもZeeman効果による直接的なCooper対の破壊に加えて、上記準粒子が磁束を周回する超伝導電流に 流される効果(Dopplerシフト)、狭くなった磁束の間を飛び移る効果(磁束格子効果)、隣接する磁束間で 超伝導電流が部分的に打ち消し合う効果、等が考えられます。ただし、これらの磁場効果は高磁場ほど顕著に なるもので、通常の超伝導体の場合、低磁場では無視できるものです。
超伝導状態を理解する上で重要な物理量としてコヒーレンス長(ξ0)と呼ばれる長さがあります。これは超伝導を担う電子対(=Cooper対)において、電子がお互いに対の相手として認めあう距離(相関距離)を意味し、フェルミ面上での電子の速度VFに比例する一方で超伝導ギャップΔ0に反比例します(ξ0~hv/Δ0)。よく知られているように、第二種超伝導体の特徴はこのコヒーレンス長がもう一つの基本的な長さである磁場侵入長λよりずっと短い(ξ0<<λ)、という点にあります。この場合、磁場中で金属全体の超伝導状態を破壊してしまうよりも、磁束量子(φ0=2.07×109G/A2)と呼ばれる量子化された磁束が超伝導体を貫通し、その部分のみで超伝導が壊れた状態の方が安定(=自由エネルギー*が小さい)になります。これを磁束格子状態、あるいは混合状態と呼びます。
ちなみに超伝導状態の本質は、対になった電子の波動関数(基本的に平面波∝exp(ikr)に比例)の空間位相が超伝導体のどの位置でもゼロになっている(krと-krが打ち消し合う)という点にあり、磁束量子はちょうどその磁束による波動関数の位相変化が2πとなってゼロと等価になるために超伝導状態と共存できるのです。また、これらの磁束は、空間的な平均の磁場が外部磁場とほぼ一致するような格子間隔で並び、格子の形も通常は三角格子であることが知られています。さて、それでは磁束一本一本を眺めたとき、超伝導はどの程度の領域で壊れているのでしょうか。図1にあるように、実は厳密に言うと超伝導ギャップがゼロになっているのは磁束の中心点(=特異点)だけで、そこから遠ざかるにつれて超伝導は徐々に回復し、ある特徴的長さξよりずっと遠方で本来の値Δ0に戻ります。このギャップの空間的な不均一さの度合いを特徴づける長さをGinsburg-Landauのコヒーレンス長と呼びます。これは初めに出てきた長さξ0と低温・高磁場の極限では一致すると考えられていますが、基本的には与えられた温度・磁場で自由エネルギーが最小になるように変化する量です。 磁場の上昇とともに磁束格子の間隔が狭まり、最終的にξより狭くなったとすると超伝導が壊れた方がエネルギー的に得になるので、この時上部臨界磁場Hc2からξの極限値ξGLがHc2=φ0/2πξGL2という関係で導かれます。
それではξ(T,H)は有限の温度・磁場でどのように変化するのでしょうか。これは現在でも未解明の部分が あるテーマの一つで、混合状態をより深く理解するために実験・理論双方から様々な研究が行われています。 まず、温度の効果として、低温ほど顕著になると予想される効果にKramer-Pesch効果というものがあります。 これは磁束付近の超伝導ギャップに図1のような空間変化があることから、Cooper対を形成していない電子 (=常伝導状態にある電子、ギャップを超えた励起子という意味で準粒子とも呼ばれる)が磁束コア付近に 離散的な束縛状態を作ることによるもので、温度のエネルギースケールがこの束縛状態の準位間隔より小さく なると低い準位のみが占有され、ξが実効的に縮むと予想されています。次に磁場の効果ですが、これは主な ものだけでもZeeman効果による直接的なCooper対の破壊に加えて、上記準粒子が磁束を周回する超伝導電流に 流される効果(Dopplerシフト)、狭くなった磁束の間を飛び移る効果(磁束格子効果)、隣接する磁束間で 超伝導電流が部分的に打ち消し合う効果、等が考えられます。ただし、これらの磁場効果は高磁場ほど顕著に なるもので、通常の超伝導体の場合、低磁場では無視できるものです。 さて、我々のグループでは、磁束状 態の磁場分布から磁束の構造を微視的に観察できるμSR法を用いてこれらの問題を研究していますが、 最近代表的な銅酸化物超伝導体の一つであるLa2-xSrxCuO4(LSCO)の低磁場中において奇妙な現象を観測したので、それについてご紹介しましょう。
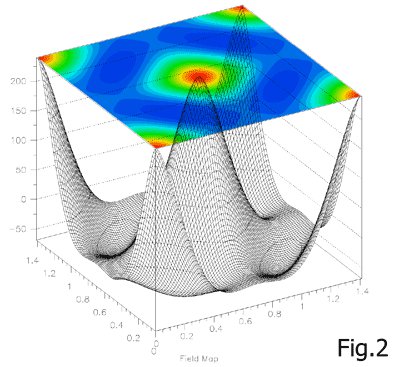
「最近の研究から?YNi2B2Cの磁束状態」の節でも紹介されているように、μSR法を用いると磁束格子状態 の空間的な磁場分布B(r)について、その平均を密度関数n(B)の形で得ることができます。 このn(B)と磁束格子の形の情報を用いると磁場分布B(r)を再構成することができます。 図2 がそのようにして再現されたYNi2B2Cの磁束格子状態における磁場分布です。この例では格子が四角格子になっ ていることが中性子小角散乱等の実験から明らかになっており、その原因としてフェルミ面の異方性のために 超伝導電流が「四角」に流れている(VFが[100]方向と[110]方向で大きく異なる)ことによると考えられてい ます。図2はそのような効果をも考慮して再構成されたものですが、実際に一本一本の磁束の周りの磁場分布 が強い四回対称性を持っており、全体として電磁エネルギーを下げるために四角格子を組んでいる様子が分かります。
さて、我々のグループでは、磁束状 態の磁場分布から磁束の構造を微視的に観察できるμSR法を用いてこれらの問題を研究していますが、 最近代表的な銅酸化物超伝導体の一つであるLa2-xSrxCuO4(LSCO)の低磁場中において奇妙な現象を観測したので、それについてご紹介しましょう。
「最近の研究から?YNi2B2Cの磁束状態」の節でも紹介されているように、μSR法を用いると磁束格子状態 の空間的な磁場分布B(r)について、その平均を密度関数n(B)の形で得ることができます。 このn(B)と磁束格子の形の情報を用いると磁場分布B(r)を再構成することができます。 図2 がそのようにして再現されたYNi2B2Cの磁束格子状態における磁場分布です。この例では格子が四角格子になっ ていることが中性子小角散乱等の実験から明らかになっており、その原因としてフェルミ面の異方性のために 超伝導電流が「四角」に流れている(VFが[100]方向と[110]方向で大きく異なる)ことによると考えられてい ます。図2はそのような効果をも考慮して再構成されたものですが、実際に一本一本の磁束の周りの磁場分布 が強い四回対称性を持っており、全体として電磁エネルギーを下げるために四角格子を組んでいる様子が分かります。