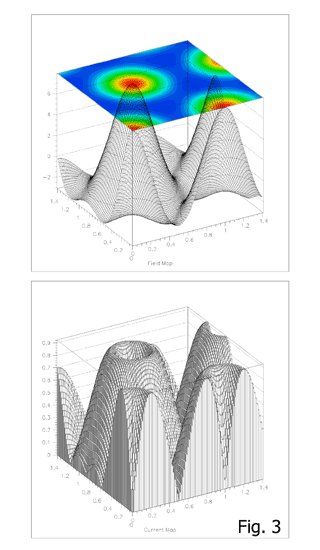
図３は同様にして得られたLSCO中の磁束格子状態におけるB(r)および超伝導電流J(r) （面内方向、Maxwell 方程式J(r)=rot B(r)から得られる）の分布です。[実はLSCOでも、少し磁場を高くすると四角格子になるらしい ことが最近分かってきたのですが、この場合のような低磁場ではまだ三角格子のようで、図３もそのように仮定 して再構成してあります。] 特徴的なのは、磁場のピーク（磁束中心）での値が相対的に小さく、磁場分 布が「鈍っている」ことで、これはJ(r)がピークを取る半径で定義される磁束コア半径ρVが大きいことに対応 します。ここで重要なことは、このρVが先程述べたξとほぼ等価であると見なせる点です。実はこのような大 きな磁束コア半径が低磁場で観察されるのはLSCOだけではなく、先のYNi₂B₂Cの例も含め他の超伝導体でも共通 した傾向です。 LSCOではさらに興味深いことに、この磁束コア半径とキャリアの濃度xとが特異な相関を示すことが分かってき ました。LSCOをはじめ銅酸化物超伝導体では、価数の異なる元素置換を行うことによりCuO₂面内にキャリア（ホールまたは電子）を注入することで超伝導が発現しますが、超伝導性も含め系全体の物性はその濃度とともに系 統的に大きく変化することが知られています。例えばLa_2-xSr_xCuO₄ではxをゼロから徐々に増やすことでホールが 注入されますが、x=0.05付近から超伝導が出始め、0.15あたりで転移温度Tcが最高値（～38K）を取り、xの増大 とともに今度はTcが減少して0.25を超えたところで消失する、という振る舞いが知られています。 特に超伝導の機構と関連して注目されるのは、金属としての性質がx=0.15付近を境にして変化していることが様 々な物理量の特徴から示唆されている点です。 そこで我々は、x=0.13、0.15、0.19という３つのホール濃度を持 つ試料について低磁場でμSR測定を行い、磁束コア半径ρV（～ξ）がホール濃度とどのような相関を示すのかを 調べてみました。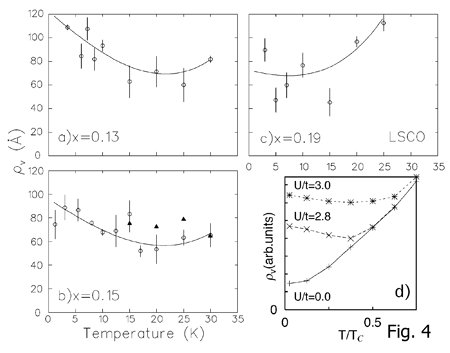 図４にそれぞれの試料でのρVの温度依存性を示します。測定点の数が十分とは言えませんが、x=0.13、0.15と 0.19で明らかに異なる傾向が見て取れます。最適ホール濃度以下の試料では温度の低下とともに一旦減少しかけた ρVが増大する傾向を示しているのに対し、過剰ホール濃度領域では単調に減少しているように見えます。後者は 先に触れたKramer-Pesch効果で定性的に理解できるのに対し、前者はこれと全く逆で、何か今までに考慮されて いない効果が現れているように見えます。さらにこれらを零度へと外挿した値ρV(0)をホール濃度xの関数として プロットしたのが図５です。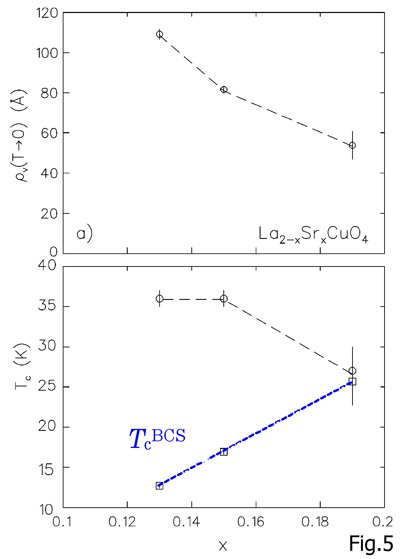こちらも通常のBCS理論に従う超伝導機構を仮定し、なおかつフェルミ速度がホール 濃度によらないとしたときに予想される傾向に反しており、過剰ホール濃度側を基準にすると最適濃度以下では 何らかの異常があると言うことができます。 このような異常を理解する手がかりとして、最近銅酸化物超伝導体で明らかになってきた「磁場誘起磁性」が あります。ストライプ的な超構造を伴った反強磁性状態が超伝導状態と共存するような基底状態が背景にある場合 、混合状態で一部超伝導が抑制されたところに反強磁性秩序が復活する（反強磁性磁束コア）ということが理論的 に予想されます。実際に磁場下で反強磁性相が誘起されるという報告も中性子回折、NMR等からなされていますが、 LSCOについては中性子による測定だけで、そのような反強磁性が磁束コアに本当に局在しているのかどうかについ ては必ずしもまだ明確ではありません。 ところで我々が観測した最適ホール濃度以下での大きな磁束コア半径は、 このような「磁束コアに局在する反強磁性相関」を考慮するとうまく説明できることが分かりました。もちろん 準静的な反強磁性が磁束コアで復活するとミュオンはその大きな磁気モーメントを見てしまいますが、図４、図５ の元になるデータはいずれも0.2テスラという低磁場であるため、反強磁性が強い揺らぎを伴った状態であるとす ると実効的な磁束コア半径の変化としてのみ観測されると理解できます。 実際、同じ試料で更に磁場を上昇させると明らかに準静的な反強磁性によると思われるスピン緩和の増大が見られ ており、このような理解と矛盾なく説明できるようです。 このように、LSCOの磁束コア半径は最適ホール濃度以下で異常に大きい値を取る傾向を示しており、このよう な磁束コア半径、すなわちGLのコヒーレンス長の実効的な増大は、基底状態の背景にある強い反強磁性揺らぎが 磁束コア近傍の超伝導の抑制とともに顔を出す傾向を持つことを示唆していると考えられます。この傾向はいわ ゆる量子臨界点近傍における磁性と超伝導の共存の様態とは趣を異にするもので、少なくともLSCOにおいてスト ライプ的な新奇な電子状態が超伝導の背景にある、ということを示唆しているということも出来るでしょう。 なお、ここに紹介した研究成果は内田慎一先生のグループ（東京大）、植村泰朋先生のグループ（コロンビア大）、町田一成先生のグループ（岡山大）その他の方々との協同研究によるものです。

詳細は"Expansion of vortex cores by strong electronic correlation in La_2-xSr_xCuO₄ at low magnetic induction "：R. Kadono, et al., Phys. Rev. B 69, 104523 (2004)を参照 * 一般的にはいわゆるヘルムホルツの自由エネルギー