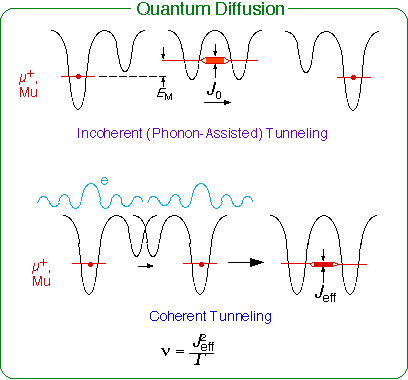
 量子拡散とは固体結晶内に置かれた原子が量子トンネル効果によって移動していく現象で、質量の軽い陽子やミュオン(陽子の約9分の1の質量)の拡散を理解する上で重要なことが知られています。特にミュオンは、陽子と比べても質量が非常に軽い粒子であるため、量子拡散の効果が顕著に現れやすく、量子拡散そのものを研究するためのユニークな実験場として大変役立っています。右の図では量子拡散がどのように起こるかを絵解きしたものですが、この図を理解する上で重要な点は、結晶格子内に置かれた原子はその周りに必ず格子の歪みや電子分布の歪み(金属中で)を伴っており、所謂「ポーラロン状態」を形成しているということです。このように、原子はいわば自分で作ったポテンシャルの中に捕えられた「自己束縛」状態にあるわけですが、中間的な温度(10-100K)では熱揺らぎにより(フォノンの助けを借りて)瞬間的に隣接する原子のエネルギー準位の縮退が起こります。すると原子はトンネル効果でポテンシャルバリアを越えることなく隣のサイトへと移動する事が出来るわけです。
しかし、更に低温ではもっと興味深いことが起こります。自己束縛状態とはいえ原子の波動関数は有限の広がりをもっており、隣接サイトの状態を表す波動関数とoverlapがあるわけですが、それはまさにトンネルマトリックスに比例した量になります。この場合、上述の熱揺らぎはそのようなoverlapを阻害する要因としてのみ働き、温度が低いほど(トンネル効果による)拡散が速くなる、という不思議な効果が見えるのです*。
量子拡散とは固体結晶内に置かれた原子が量子トンネル効果によって移動していく現象で、質量の軽い陽子やミュオン(陽子の約9分の1の質量)の拡散を理解する上で重要なことが知られています。特にミュオンは、陽子と比べても質量が非常に軽い粒子であるため、量子拡散の効果が顕著に現れやすく、量子拡散そのものを研究するためのユニークな実験場として大変役立っています。右の図では量子拡散がどのように起こるかを絵解きしたものですが、この図を理解する上で重要な点は、結晶格子内に置かれた原子はその周りに必ず格子の歪みや電子分布の歪み(金属中で)を伴っており、所謂「ポーラロン状態」を形成しているということです。このように、原子はいわば自分で作ったポテンシャルの中に捕えられた「自己束縛」状態にあるわけですが、中間的な温度(10-100K)では熱揺らぎにより(フォノンの助けを借りて)瞬間的に隣接する原子のエネルギー準位の縮退が起こります。すると原子はトンネル効果でポテンシャルバリアを越えることなく隣のサイトへと移動する事が出来るわけです。
しかし、更に低温ではもっと興味深いことが起こります。自己束縛状態とはいえ原子の波動関数は有限の広がりをもっており、隣接サイトの状態を表す波動関数とoverlapがあるわけですが、それはまさにトンネルマトリックスに比例した量になります。この場合、上述の熱揺らぎはそのようなoverlapを阻害する要因としてのみ働き、温度が低いほど(トンネル効果による)拡散が速くなる、という不思議な効果が見えるのです*。
* 最近の総説としては、たとえば, R. Kadono, Applied Magnetic Resonance 13, 37-54 (1997)を参照。
理論的予想 vs 実験例
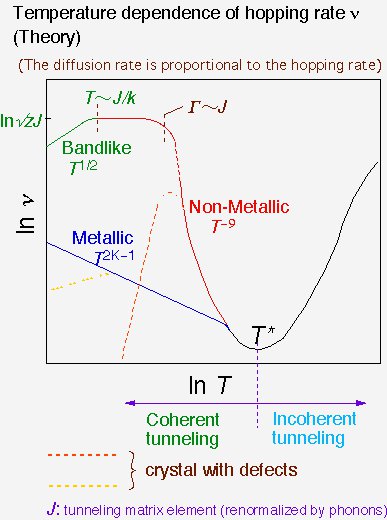
This picture is a summary of theoretical predictions on the temperature dependence of hopping rate in crystalline solids: a steep increase of the hopping rate is expected in insulating crystal, whereas much more moderate temperature dependence is expected in metallic environments due to the Ohmic damping of tunneling motion.
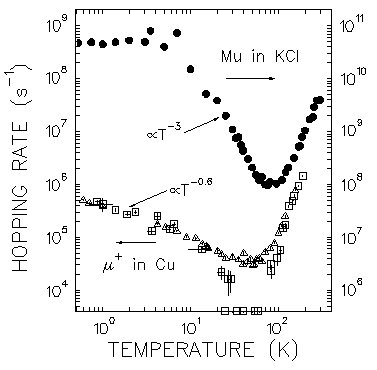
This picture shows two memorial data sets of muon diffusion in high-purity copper (Kadono et al., 1989; Luke et al., 1991) and muonium (Mu) diffusion in KCl (Kiefl et al., 1989; Kadono et al., 1990; MacFarlane et al., 1994). Note that the scale of the vertical axis is very different between these two (i.e., muonium diffusion in KCl is faster than muon in copper by orders of magnitude, indicating that the tunneling matrix element for muonium in KCl is quite large).