超伝導体のもつ著しい性質の一つとして、いわゆるマイスナー効果というものがあります。これは超伝導体を磁場中に置いたときに、 ある臨界磁場以下では超伝導体のごく表面を除いて内部に磁場が入らない現象で、超伝導体内部に丁度外部磁場を打ち消すような磁場を 作り出す永久電流が流れるために起こる現象です。ところで超伝導体はこの臨界磁場以上の磁場に対する応答の仕方によって大きく2種 類に分けられることが知られており、超伝導が完全に破壊されてしまうものを第一種超伝導体、磁場が規則正しく並んだ磁束の状態で超 伝導体内部に侵入し、磁束の外側の領域で超伝導を保ち続けるものを第二種超伝導体と呼びます。第一種超伝導体の臨界磁場は数百ガウ ス程度と比較的低いのに対し、第二種超伝導体の超伝導が完全に破壊される磁場はその数百倍に達し、銅酸化物高温超伝導体に至っては 測定不能なほど高いことが知られています。これは応用上大変重要な意味を持ち、高磁場用超伝導マグネット等はすべてこの第二種超伝 導体の発見によって可能になったと言えます。 磁束状態では磁束が三角格子（場合によっては正方格子）を組んで二次元的に並んでおり、更に一本一本の磁束を眺めると、磁束の 中心には半径一定（コヒーレンス長ξ）の常伝導状態のコアがあり、コアの外側の磁場は周りの超伝導電流によって磁場侵入長λ程度に 押さえ込まれているというのが従来の理解でした。ところが最近の様々な研究から清浄極限にある超伝導体中ではどうもこのような単純 な描像は成り立たないことが明らかになりつつあります。その一つの現れが、磁場とともに磁束のコア半径が伸縮するという現象です。 最近見つかった超伝導体ErNi₂B₂Cの磁束状態の観察。このような磁束状態にミュオンを注入すると、ミュオンはランダムに磁場分布 をプローブし、磁束の周りの磁場分布を反映したスピン回転の周波数分布を示す。上図にあるように、磁束状態にある超伝導体中にミュ オンを注入すると、磁束の周りの磁場分布を直接測定することができます。そこで磁場分布の高磁場側を見ると、その最大値は磁束コア の半径で決まっている事がわかります。そこで、最近発見された比較的Tcの高い超伝導体であるYNi₂B₂CについてμSRの測定により磁束 コアの大きさが磁場とともにどのように変化するのかを調べました。

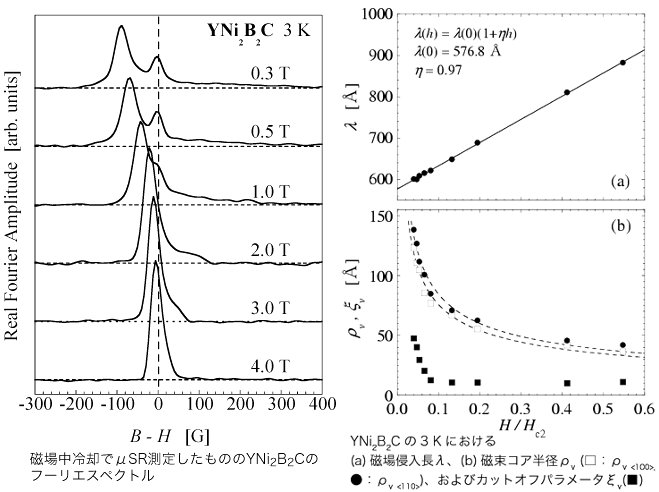
左図はμSRの時間スペクトルをFFTにより周波数スペクトルに変換したもの（実部）で、横軸（周波数をミュオンの磁気回転比2π 135.5MHz/Tで割った値）は磁場に相当しており、これが混合状態での磁場分布を示しています。Hは印加磁場で、B - H=0 の部分にピークがあるのは試料の外にとまったミュオンからのバックグラウンドに対応します。この図で特に高磁場側を注意すると、磁束コアでのカットオフが明瞭に見られます。

これらのデータと、カットオフ及びnonlocal補正を取り入れたLondonモデルで磁束とその周辺の磁場分布を計算したものとの比較か ら磁場侵入長及びコア半径を求めると上右図のようになり、磁場とともに磁場侵入長は増大する一方で、コア半径が急激に減少している ことが分かります。このような磁束コアの収縮は古典的な理論では予想されない振る舞いであり、現在理論的にも活発な議論が行われています。 詳しくは K. Ohishi et al., Phys. Rev. B 65, 140505R (2002).