- Topics
[For researchers] Deep learning methods for parameter space sampling
August 6th, 2025
Finding the optimal point that satisfies conditions in phenomena with many variables often requires enormous computing time. Ahamed Hammad, a researcher at the Institute for Particle Physics and Nuclear Physics(IPNS), KEK, and Raymundo Ramon, a researcher at Korea Institute for Advanced Study (KIAS) have released DLScanner, a package that accelerates this scanning process by combining deep learning with a numerical integration method called the VEGAS method. This method is expected to be effective for all problems with many free parameters and that require high computational costs.
-
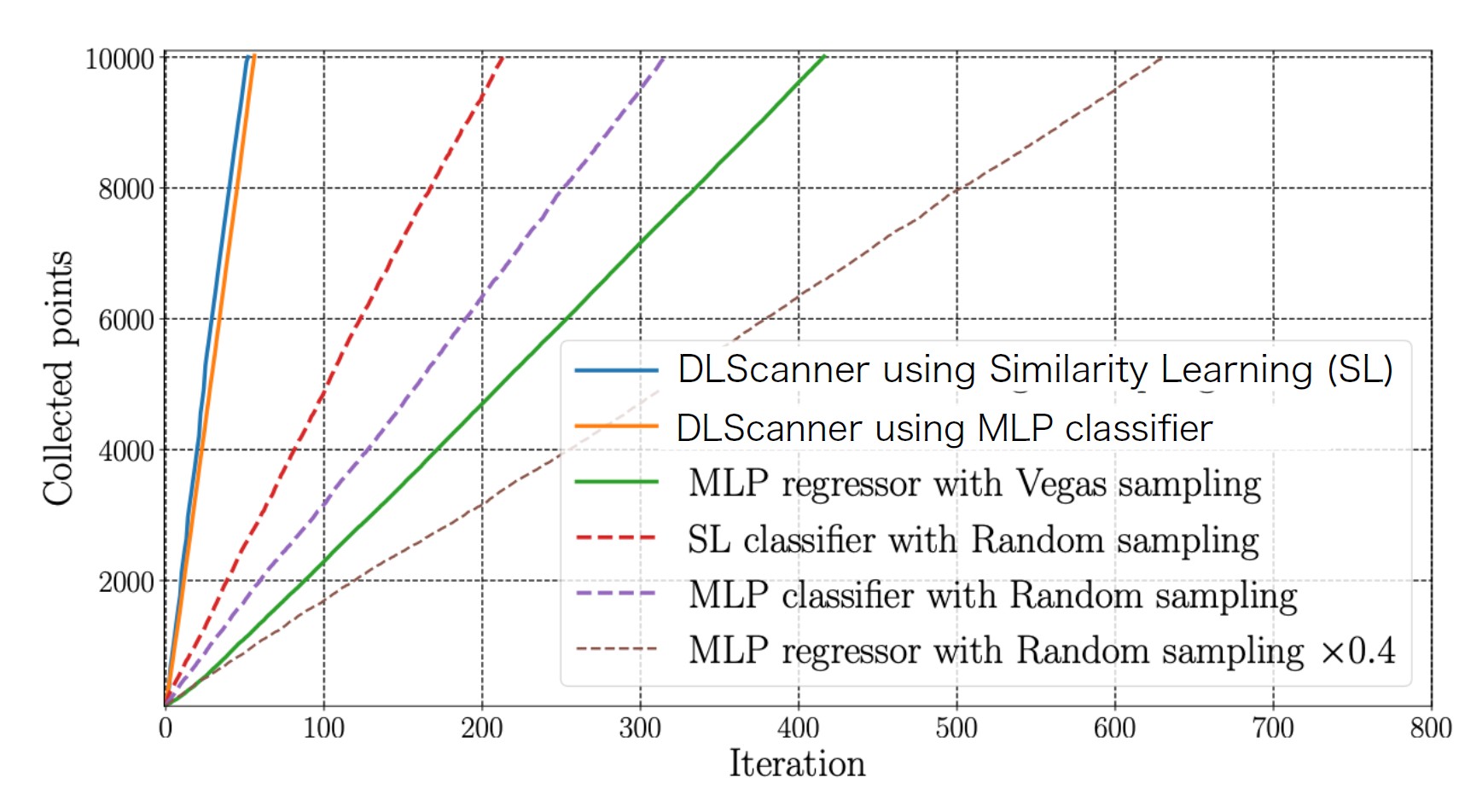
Comparison of variable exploration using DLScanner (combining VEGAS sampling and deep learning classifiers) in this study and variable exploration using random sampling. As the number of iteration steps (horizontal axis) increases, the number of effective sample points for variable scanning (vertical axis) also increases. However, DLScanner (blue or orange solid lines) collects effective samples with fewer iterations compared to random sampling or regression-based algorithms.
Core idea
Scanning high-dimensional parameter spaces that satisfy given conditions is both computationally expensive and time consuming. Can deep learning techniques be used to improve the efficiency of this process? A neural network can learn a complex, high-dimensional mapping between the input sampling space and the desired target region. Once trained, it can rapidly predict parameter values that are likely to satisfy the required constraints. The result is a powerful tool for accelerating the exploration of high-dimensional parameter spaces, even in scenarios where individual evaluations are computationally intensive.
Overview
Over the years, diverse strategies have been developed to explore complex parameter spaces that satisfy physical interest, defined by compatibility with theoretical and experimental constraints. The simplest among them are grid and random sampling, which can explore the entire space. However, these methods are often inefficient, as they converge slowly toward regions of interest, limiting their practical usefulness. In contrast, adaptive sampling techniques offer a more targeted approach to guide the search toward target regions by iteratively maximizing the likelihood function. These methods, such as Markov Chain Monte Carlo (MCMC) and MultiNest, can concentrate computational resources on the most promising areas of the parameter space leading to a fast convergence to the target region. However, they can still struggle in complex regions of the parameter space, especially those with sharp features, irregular structures or degenerate regions of interest. These challenges may lead to inefficient sampling, resulting in excessive likelihood evaluations or poorly explored areas.
Ahamed Hammad and Raymundo Ramos recently proposed DLScanner, a new adaptive sampling algorithm using Deep Leanring (DL) methods. DLScanner offers a flexible and powerful alternative to accelerate parameter space exploration. It operates through iterative training of a neural network, where the network is continuously refined using a growing dataset of sampled points predicted by the network itself. As training progresses, the network becomes increasingly effective in predicting new candidate points that are likely to satisfy the desired constraints, thereby streamlining the search process in highly computationally demanding and high-dimensional settings.
Methodology
-
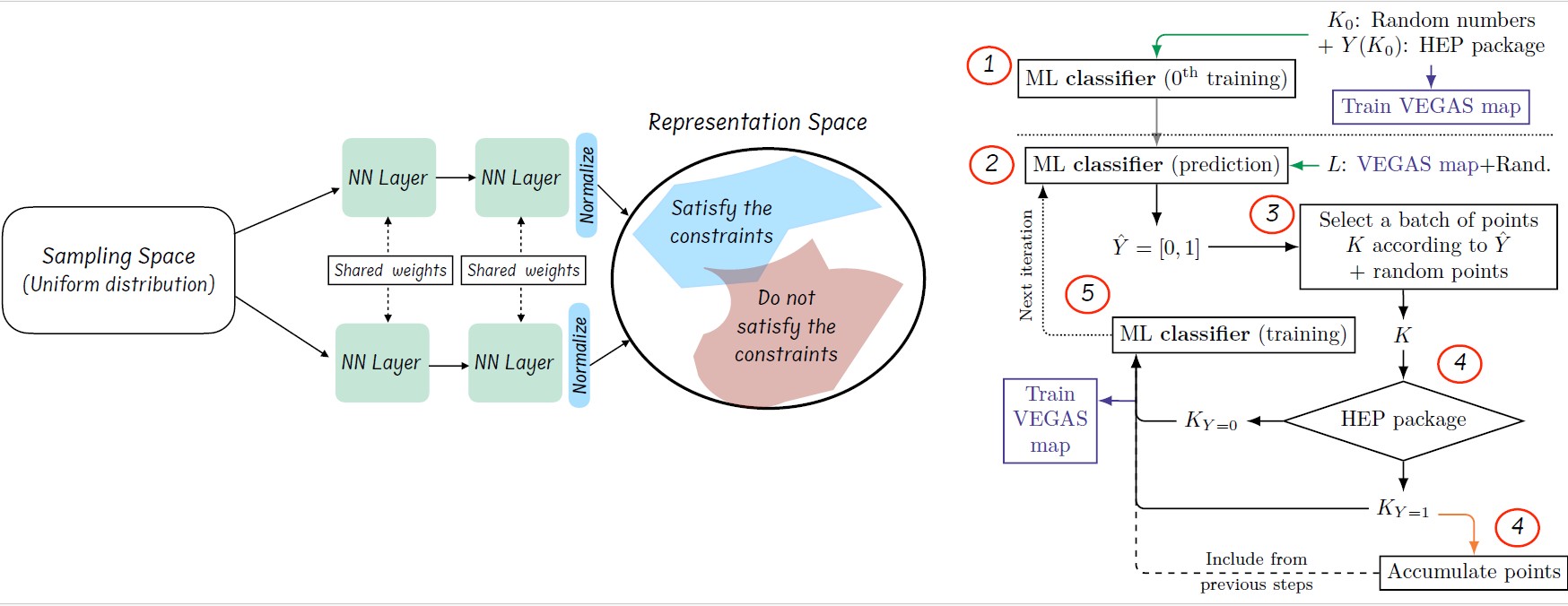
Figure 1: The left plot highlights the role of similarity learning in improving the mapping between the sampling space and the target region, while the right plot depicts the complete scanning loop.
The proposed scanning approach has two key components:
• Similarity Learning Network:
This network is designed to map sampled points into a latent representation space. Points that correspond to valid regions of the parameter space are clustered together in the representation space, while those that do not satisfy the target constraints are pushed further apart, as shown in the left plot of figure 1. This representation enhances the convergence ratio of the network toward the generation of valid points, as it allows the network to learn an efficient parametrization of the geometry of the representation space.
The network is trained to minimize a contrastive loss function, which shapes the structure of the representation space into a hypersphere, encouraging a larger Euclidean distance between valid and invalid points.
• Dynamic Sampling:
To generate points efficiently in regions of interest, a VEGAS mapping, traditionally used for adaptive multidimensional integration, is integrated into the scanning loop. The VEGAS algorithm is rewritten to facilitate point generation near the target regions, accelerating convergence. An illustrative animation of the application of this method for a two dimensional donuts shape,
F2d (x1, x2)= [2 + cos(x₁)⁵·cos(x₂)⁷]⁵, with the target points should satisfy the condition of F2d = 100 ± 5, can be found this repository.
The full scanning process involves several iterative steps, as illustrated in the right plot of Figure 1, where the red circles indicate the following steps:
1. INITIALIZATION: An initial set of random points in the parameter space is generated and used as a training data set.
2. PREDICTION: The trained deep learning network is used to predict values for a large set of random points. This process is fast and numerically low cost because it is network evaluation.
3. SELECTION: A subset of points is selected based on predetermined criteria reflecting the constraints to the desired region.
4. REFINEMENT: The value of the selected parameter points is evaluated, and the true values are compared against the model predictions. The point that prediction and true values match sufficiently is added to the refined dataset.
5. NETWORK UPDATE: The DL network and VEGAS are retrained using the refined dataset to enhance its capacity to predict future points accurately.
6. ITERATION: The loop continues to generate new points and train the network and VEGAS iteratively.
Applications
The proposed scanning method has broad applicability across various disciplines that require identifying points in high-dimensional parameter spaces that satisfy specific constraints. For example, in particle physics, it can be used to scan the free parameters of the scalar potential in the Two Higgs Doublet Model, such as mass parameters and couplings. The task is to find the region of the mass and coupling parameters that satisfy all theoretical and experimental constraints. Evaluating the values of physical predictions under the various theoretical and experimental constraints using HEP packages takes approximately 9 seconds. For a grid search of the points that satisfy the constraints, the total computation time scales as 9 × nd, where “n” is the step per parameter and “d” is the number of free parameters. Applying MCMC to this problem typically requires 140 iterations of the HEP packages, with 100 points evaluated at each iteration, resulting in a total runtime of 140 × 100 × 9 seconds. In contrast, our approach achieves the same goal with only 75 iterations, reducing the total scanning time to 75 × 100 × 9 seconds. DLScanner can handle up to 40 parameters, while it is not easy for MCMC.
Published paper
DLScanner: A parameter space scanner package assisted by deep learning methods,
A. Hammad and Raymundo Ramos
Arxiv: 2412.19675 [hep-ph]
Comput.Phys.Commun. 314 (2025) 109659
Public code
The code is published in Python Package Index:
https://pypi.org/project/DLScanner/
Installation:
pip install DLScanner== 1.0.0







