昨年のノーベル物理学賞で脚光をあびた「対称性の破れ」って、考えてみるとヘンな言葉ですね。「対称」という言葉からはベルサイユ宮殿やインドのタージマハールのように「美しい」と感じる建物が思い浮かぶかもしれません。でも、対称性が「破れる」ってどういうことでしょう?
物理学の世界では、物体の運動や反応の法則を数式で表します。二人でキャッチボールをしている姿を鏡に映してみると、右投げと左投げの区別は付きますが、ボールの動きだけを見ていると、実際の映像と鏡に映してみた映像の区別がつきません。これはボールの運動を表す数式が、鏡に映す(左右を入れ替える)という操作に対して「対称」になっているからです。
物理学で出てくる数式が、どんな場合に対称性が保たれているのかを、物理学者はとても気にします。対称性が保たれている数式からは、ある大事な法則が導かれるからです。ここでいう「対
称」は、鏡に映るような「左右対称」だけではありません。例えば東京でキャッチボールをしても、大阪でキャッチボールをしても、ボールの動きを表す数式は変わりません。これを「空間の平行移動に対して対称」といいます。
この空間移動の対称性から、運動量の保存則という物理学にとって大事な法則が導かれます。回転する物体に対しても、物体がどっちを向いている時でもその動きを表す数式が同じ場合、角運動量の保存則が導かれます。
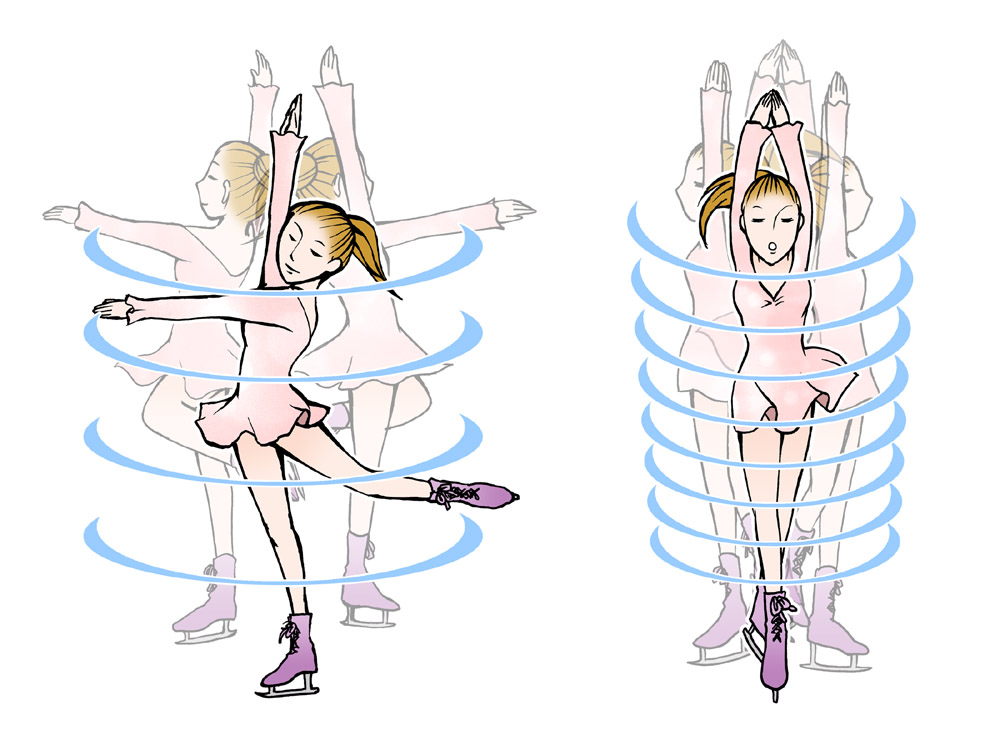
氷の上でフィギュアスケーターがスピンをする時、腕を大きく拡げて回転しながら身体に近づけると、回転の速度が上がります。これも角運動量の保存則で説明することができます。
空間の性質や数式が空間をどの向きで眺めても変わらない。一見あたりまえに見えることが、物理学の大事な法則と関係してきます。そこで物理学者は「対称」ということにとてもこだわるのです。
対称性が崩れている時には、その対称性から導かれた物理の保存則も成り立たなくなります。物理学の掟を破っているから「対称性の破れ」? 物理学者の言語感覚って、不思議ですね。