2012B(平成24年11月~平成25年3月)の一般利用公募が、平成24年5月17日(木)~平成24年6月7日(木)の期間に行われた。2012Aを100件程度上回る約250件の応募があった。
伊藤晋一氏が、6月1日より教授に昇任した。
SuperHRPDは、一通りの装置コミッショニングを終え、通常の室温測定においては一般ユーザー課題を受け入れ始めている。現在、冷凍機などの試料周辺機器のオンビームでのコミッショニングが始まり、4K冷凍機では、実際にRietveld解析を行える環境が整った。
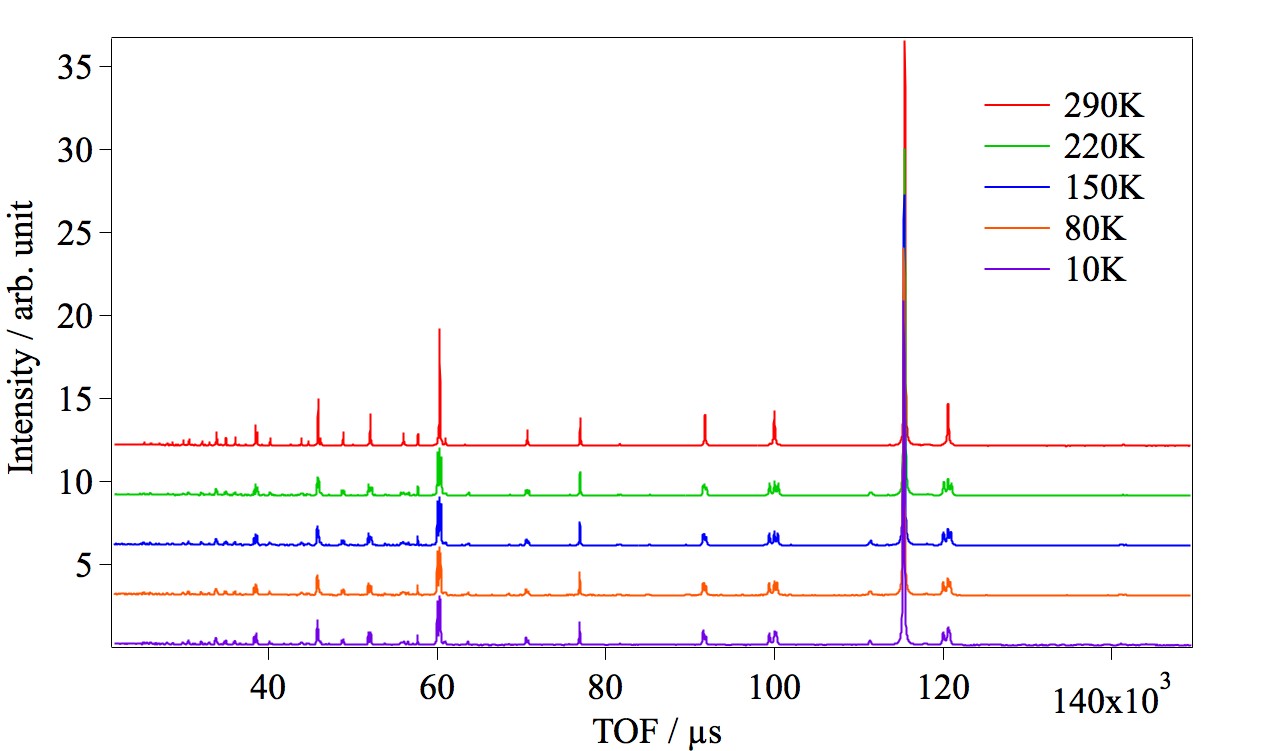
図1. Li電池材料の低温測定
引き続きJ-PARC MLFの革新型蓄電池棟内で、回折計本体の組立作業を行なった。これまでに回折計本体のフレームを組み立てがほぼ終了したが、6月後半のビームタイム中に中性子回折実験を実施するため、背面散乱バンクを中心に設置作業を進めている。現在、6月18日から実験を開始できるように、散乱槽内の遮蔽材貼り付け、入射ダクト調整作業等の工事を急ピッチで実施している。

図2. BL09の検出器バンク取り付け作業
1. 課題実施状況
SOFIA反射率計はRun#42後半(5/1-25)でプロジェクト課題3件(22日)を実施した。
2. 装置開発状況
SOFIA反射率計では半導体光検出素子MPPC(multi-pixel photon counter)を用いた高位置分解能1次元検出器の開発をDAQグループと進めている。図3の(a)および(b)に示す通り、検出器1ユニットあたり32個のMPPCを配置しており、抵抗分割方式で位置検出を行う。有感領域は120mm×5mmで、これを20本並べることで120mm×100mmの領域をカバーすることが可能である。1本あたりの係数率はシンチレーター(6LiF/ZnS)の残光が消失する時間で決まるため10-20kcps程度とこれまでの検出器と変わらないが、中性子反射率計は幅の広いビームを用いるため、トータルの係数率を最大20倍まで増やすことが可能である。ただし、1軸方向には高い分解能が必要であり、この検出器では1mm以下の分解能を目指している。
昨年度の3月には1ユニットのテスト実験について報告を行ったが、その後20ユニットを並べた検出器を作成し、実際に導入を予定しているSOFIA反射率計で行った。20ユニットを組み上げた写真は図3(a)の通りで、これに遮光用のアルミカバーをかぶせて実験を行った。図4は0.1 mm (V) × 50 mm (H)のビームに対して6 mmステップでスキャンを行った結果で、それぞれの検出器が1 mm程度の分解能で働いていることを確認できた。ただし、電気ノイズやADコンバーターで発生する熱によるゲインの変化(MPPC検出器は温度によってゲインが大きく変化する)により検出器の端で特性が悪くなっていることが分かった。これらの問題解決への目処はついており、近いうちに対応を行う予定である。
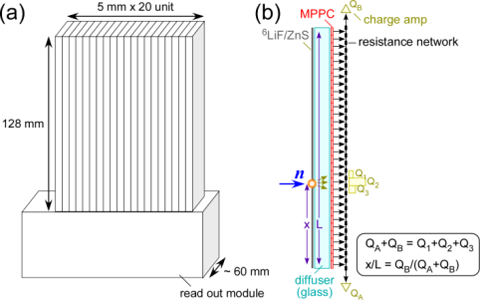

図3. BL16用MPPC検出器の(a)模式図と(b)検出方式、および(c)組み上げた検出器の写真
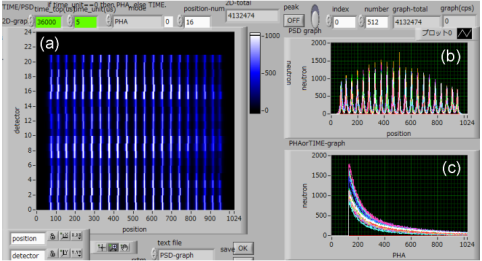
図4. BL16にて行ったビームスキャンの結果。(a)20本の検出器により得られた2次元イメージ、(b)1軸方向への射影、(c)波高値の分布。
研究成果
"Quantum renormalization effect in one-dimensional Heisenberg antiferromagnets",
S. Itoh, T. Yokoo, S. Yano, D. Kawana, H. Tanaka and Y. Endoh,
J. Phys. Soc. Jpn. 81 (2012) in press.
磁性体では結晶中の磁性原子のスピンが相互作用しているが、一次元磁性体は、特定の結晶軸に沿った磁気相互作用のみが大きく、それに対して他の方向の磁気相互作用が無視できる系である。一次元反強磁性体のダイナミクスはこれまでに多くの研究が積み重ねられていて、特に磁性原子のスピン量子数Sが1/2の場合に生じる量子効果は非常によく理解されてきた。基底状態は、古典的反強磁性状態(ネール状態)ではなく、シングレットスピン状態であり、そのため、第一励起状態は、ネール状態からの励起であるスピン波よりも、励起エネルギーが増大する。この効果は量子再規格化効果(quantum renormalization effect)として知られていて、古典論的スピン波エネルギーに対する、励起エネルギーの増大比は量子再規格化因子Rと呼ばれる。S=1/2の場合はR=π/2であることが、理論的にも実験的にも明らかになっている。古典論的スピン波の分散関係はE(q)=4SJ|sin q|であり、S=1/2 の磁気励起ではE(q)=πJ|sin q|であるので、これをE(q)=4SRJ|sin q|と書けば、R=π/2である。ここでJは交換相互作用定数と呼ばれ、磁性原子のカップリングの強さを表わす。次には、より一般的に、量子効果がSの値に対してどのように記述されるかという問題に興味が移る。その視点で、Sが整数の系ではゾーンセンターに磁気励起のギャップが生じるが、半整数の系では生じないという、ハルデン予想が重要なマイルストーンであった。ハルデン予想に触発され、S=1の系が集中的に調べられ、ハルデン予想は実験的にも確認された。一方でS=5/2の系のダイナミクスは古典論で記述されることが古くから知られている。S=1とS=5/2をつなぐ実験データはほとんどなく、これまでKENS(つくば)とISIS(日英協力)を用いて、一次元ハイゼンベルク型反強磁性体CsNiCl3(S=1)、CsVCl3(S=3/2)、CsVBr3(S=3/2)、CsCrCl3(S=2)のパルス中性子非弾性散乱実験を行なってきた。最近、高分解能チョッパー分光器HRCが完成したので、CsVCl3(S=3/2)をHRCでも測定し、実験データを更新するとともに、未解析だったデータも新たに解析し、この研究の実験精度を向上させた。
チョッパー分光器では磁気励起の動的構造因子S(q,E)が測定でき、そのピーク位置から分散関係E(q)が決定でき、E(q)から量子再規格化因子と交換相互作用定数の積RJが決定できる。Rを決定するためにはJを別の方法で決定する必要がある。S=1/2と1に対しては磁化率の温度変化を記述する量子論があるので、磁化率からJを決定することができるが、S=3/2と2に対しては適当な理論がない。しかし、S(q,E)をエネルギー積分して得られる静的相関関数S(q)の線幅である逆相関長の温度変化κ(T)は、各Sごとに量子論で表現されていて、κ(T)からJを決定することができる。原理的にはチョッパー分光器で測定されるS(q,E)からκ(T)を導出することによってJが決定できるが、必要なq分解能を得るために、適宜、異なるパルス中性子分光器を用いた。本研究ではパルス中性子非弾性散乱実験のみでコンシステントな結論を得た。
図5はHRCで測定したCsVCl3(S=3/2)の励起スペクトルである。入射中性子エネルギーをEi=100meVに選び、励起の全貌をブリルアンゾーン全域で測定した(a)。この実験ではマルチEi法によりEi=15meVのデータも同時に測定されていて(b)、(a)で分解能の限界以下の低エネルギー領域の励起が(b)で観測することができた。図6に各系で測定された磁気励起の分散関係E(q)を示す。sin曲線に誤差棒がついているものは、S(q,E)から導出したκ(T)から決定したJを用いて計算される古典論スピン波の分散関係である。ゾーン境界(q=0.5rlu)でのE(q)の古典論スピン波エネルギーに対する比をRとして図中に記した。得られたRは量子モンテカルロ法による理論計算の結果RQMCに一致した。スピン量子数Sの増大とともに量子再規格化効果が小さくなっていくことが実験的かつ定量的に明らかになった。
この研究は、標記の論文にまとめて投稿していたが、最近、論文掲載が決定された。これは、HRCでの研究成果が論文掲載されるはじめてのものである。
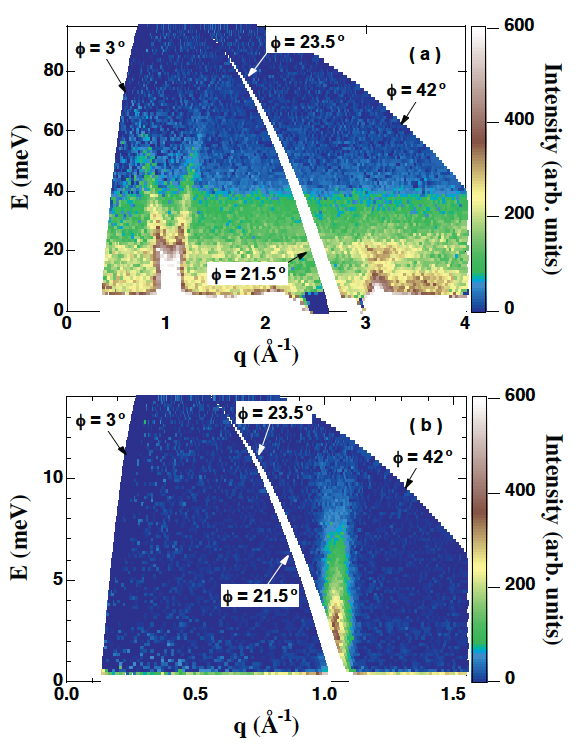
図5. HRCで測定したCsVCl3の励起スペクトル(T=20K)。(a) Ei=100meV、(b) Ei=15meV。
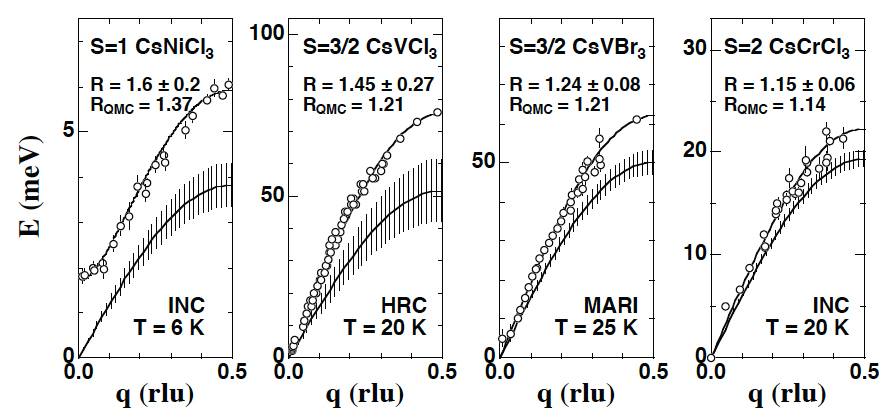
図6. 一次元ハイゼンベルク型反強磁性体CsNiCl3(S=1)、CsVCl3(S=3/2)、CsVBr3(S=3/2)、CsCrCl3(S=2)の磁気励起の分散関係(還元ゾーン形式)。sin曲線に誤差棒がついているものは、古典論スピン波の分散関係であり、誤差棒はJの誤差による。
ナノ粒子の構造解析
水素貯蔵材料の反応速度を向上させるために粒子サイズを小さくするナノ粒子化がしばしば行われる。ナノ粒子の場合、原子対相関距離と粒子サイズが同程度になるため、バルクの場合と比べG(r)の強度はrの増大とともに減衰する。またG(r)の減衰は装置分解能によっても生じる。 プログラムPDFguiでは、球状ナノ粒子の粒子サイズおよび装置分解能による減衰効果の双方をパラメータとしてデータ解析を行うことができるが、粒子サイズによる減衰効果を正確に求めるためには2つの減衰効果を分離する必要がある。そこでまずはバルクのAl2O3標準試料を用いて、NOVAの90度バンクでの装置分解能による減衰パラメータを決定した。そのパラメータを固定しさらに球状粒子を仮定して、TiO2ナノ粒子の粒径をパラメータとしてフィッティングを行った(図7)。得られた粒径は7.3 nmであり、電子顕微鏡で観測された値(約7 nm)とよく一致している。
以上よりナノ粒子化した場合の構造解析も可能であることが実証された。
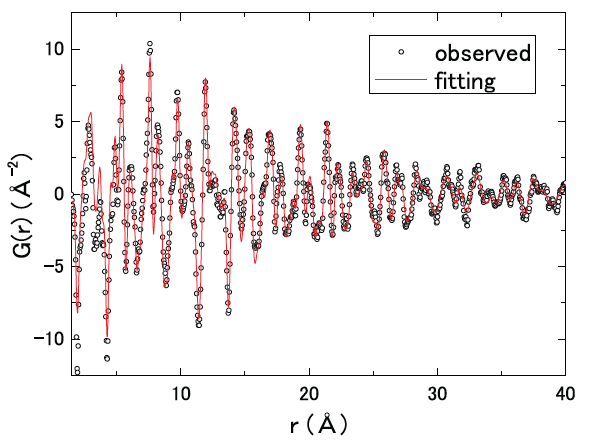
図7. NOVAにより観測されたTiO2ナノ粒子のG(r)