私にスピンをわからせて! スピンオフ問答 ~ 波動関数 たし算がかけ算に ~
物構研トピックス
2021年12月28日
「私にスピンをわからせて!」(わたスピ)からスピンオフしたコラムのコーナーです。
本筋のスピンの話からは脱線するけれど、制作過程で飛び出した、わたスピ読者にぜひ聞いてほしいお話です。
波動関数 たし算がかけ算に

シュレディンガー方程式は、
わたスピ4の冒頭でやりました。

ほんとだ、「電子の状態を表す量」って書いてあるわ。
あら、でも電子じゃなくて陽子の話をしていて波動関数が出てきたわ。これっておかしくない?

確かにわたスピ4では、主に電子を取り上げてスピンや量子力学の話をしたけど、量子力学は、電子だけのための力学ではないんだよ。
量子に一般的に成り立つものとして数々の理論や実験が繰り返されて作られたものなんだ。
だから正確には、波動関数は「量子の状態を表す量」ということになるね。

へぇ、電子以外にもあてはまるのね、世界が拡がった感じがする。
じゃあ、「量子」ってなんなの?

量子とは、波と粒の両方の性質を持つような小さいもの、と考えてもらったらいいと思うよ。
具体的には、素粒子や素粒子が数個集まったものなどだね。
電子は、最も身近な、量子の代表例だった、ということ。

波の性質を持つ粒か~。
陽子も量子なの?

もちろん答えは「はい」です。
ただ、私たちのような物理学者は、すべての粒子や物質は量子力学に支配されていて、その「近似」として古典力学が見えていると考えているんですよね。

ありゃ。じゃあ、さっきのは愚問だったわけね。
量子力学が精密で、古典力学は大雑把ってこと?

大きなものに量子力学を適用しても結果は同じになるけど、そんな面倒なこと誰もしないね。

でも、すべての物質は波の性質を持つ、と言われてもピンとこないわ。

確かにそうなんですよ。

スケールが大きくなると波としての性質が現れにくくなるから、量子らしさは見えにくくなるね。

なるほどね。
量子らしさが見える大きい方の境界はどのへんなの?

大きい方の境界は、粒だと思っていたものが、波特有の
干渉の性質があるかどうか、で判断できる。過去にあいまいな状態だった領域が、実験と理論が合っていって少しずつ狭まっていったという経緯があるよ。

へぇ、どんな実験?

二重スリット実験で、干渉縞が見えるかどうか、という実験です。
はたしてどれくらいの大きな系まで、いわゆる量子力学の「干渉効果」が見えるかということは今でも挑戦されているんですよ。
フラーレンと呼ばれるサッカーボール型の炭素の分子C60などで干渉効果が見えたそうです。

じゃあ、陽子が波の性質を持つかどうか、実験で確かめたことはあるの?

うーん。
低エネルギーの陽子を使って二重スリットの実験をするのは難しそうですね。

KEKは陽子の加速器も扱っているんじゃなかったっけ?

もちろん、いまは東海村のJ-PARCで陽子を実験に使っていますけど、J-PARCはその名の通り「大強度陽子加速器施設」で、扱うのはエネルギーの高い陽子です。
逆に、量子力学の効果が見えるような小さなエネルギーの陽子をコントロールすることは難しいんですよ。

ふ~ん、そんなものなのね。

ですが、陽子は非常に小さくて、問題なく量子力学が使える領域です。
だから、陽子でも、安心して波動関数を使ってください。

はぁ、安心して使います。
・・・って、どういうこと?

それをこれから説明しますよ。
式を先ほどのように日本語で書いてもいいですか?

もちろん。
日本語の式なら意味が分かりやすいから歓迎です。

よかった。じゃ、これで行きましょう。
シュレディンガー方程式はこんな形をしています。
(演算子)(ある波動関数)=(固有値)×(ある波動関数)
これを
固有値方程式と呼びます。

ところで、
演算子ってなんなの?

+とか-とか×とか÷とか、のことにゃ。

それは算術演算子だね。一口に演算子と言ってもいろいろあるんだよね。

<とか=とか and とか or とかのこともあるニャ。

それはプログラミングでも使われる演算子だね。いままで出てきたのは数学的な演算子だよ。
物理学でいう演算子は、例えば位置を一定距離だけずらす、とか、時間を一定時間進ませるとか、ある角度だけ回転させるとか、そういう作用をする関数なんだ。命令といってもいいね。

ふうん。アクションを示しているわけね。
なんとなくイメージできてきたような、こないような。

例えば、こんな感じ。
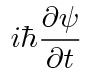 ψ
ψ以外の部分が演算子にあたるよ。量子力学では、エネルギーを演算子化したものを波動関数に作用させると考えるんだ。

なるほど。掛け算みたいで掛け算ではない。
シュレディンガー方程式の左辺は、量子の状態にエネルギーを作用させるって意味なのね。
じゃあ、右辺の
固有値ってなんでしょう?

物理量を表す0じゃない実数です。
あ、でも、0じゃなければ何でもいいわけじゃなくて、演算子が作用すると自身の定数倍になるような特別な数です。

ふうん。
エネルギーが作用すると、何倍になるの?ってこと?

そうとも言えますね。
では波動関数の考え方を使って、水素分子を考えましょう。
ちょっと頭の体操がてら準備をしましょうか。
いま、独立な変数をもつ関数1と関数2があって、
(演算子1)(関数1)=(固有値1)×(関数1)
(演算子2)(関数2)=(固有値2)×(関数2)
が成り立つとしましょう。

「独立な変数をもつ」2つの関数ってどういう意味?

例えば、1の式が分子の重心運動の話、2の式が分子の回転運動の話だと思ってください。
重心運動で変化するのは長さと時間だけど、回転運動なら角度と時間だね。
分子は重心の移動をしながら回転運動もするけど、働く力や運動の向きが違うから2つは切り離して考えることができる。

長さと角度は互いに独立しているという意味かなぁ。

そう、この変数の違いがポイントです。
さて、この2つの式の左辺と右辺に同じものをかけても式は成り立ちますよね?

はい、成りたちます。

じゃあ、1の式には(関数2)をかけて、2の式には(関数1)をかけましょう。

関数に関数をかけるの?

そうです。
(ax+b)(cx+d)みたいな感じで。
じゃあ、計算してみて。


(日本語の式ならOKとは言ったけど、計算しろだって…( ノД`)シクシク…)

え?何か言いました?

いえ、何も。
だけど先生、同じ字を何度も書くのが大変です。

ですよね。
数式は記号だらけで分かりにくいと言われますが、記号を使わないとそれはそれで不便なんですよ。
じゃあ、記号を使いましょう。
(演算子1)は
H1
(関数1)は
ψ1
(固有値1)は
E1という要領で置き換えてみましょう。

はいっ!
これなら楽だわ。

1の式と2の式はこうなりました。

この2つの式の左辺同士を足し合わせたものは、右辺同士を足し合わせたものと等しい、
ですね?

式ごと足し算するのね。
はい、等しいです。
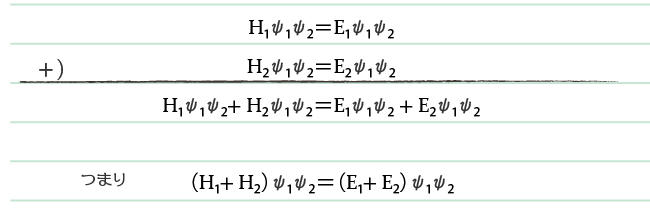

元の式と同じ形になったにゃ~。

そうですね。
同じようにして、式が3つあっても、それぞれの関数がそれぞれ全く異なる変数からなれば、このように、演算子の和と固有値の和を使って3つの式を足し合わせることができますね?

はい、同じように書けると思います。
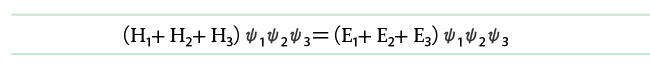
こういうことよね?

その通りです。
元の式と比べると、エネルギーは足し合わされていて、波動関数は掛け合わされていることが分かります。

ほんとだニャ~。

つまり、固有値のたし算
E1+E2+E3に対応する波動関数は
かけ算
ψ1ψ2ψ3になるってことね。

はい。
ただし、これが成り立つのは「それぞれの関数がそれぞれ全く異なる変数からなるとき」に限られますよ。
関連記事:物構研トピックス「私にスピンをわからせて!」

 シュレディンガー方程式は、わたスピ4の冒頭でやりました。
シュレディンガー方程式は、わたスピ4の冒頭でやりました。 ほんとだ、「電子の状態を表す量」って書いてあるわ。
ほんとだ、「電子の状態を表す量」って書いてあるわ。 確かにわたスピ4では、主に電子を取り上げてスピンや量子力学の話をしたけど、量子力学は、電子だけのための力学ではないんだよ。
確かにわたスピ4では、主に電子を取り上げてスピンや量子力学の話をしたけど、量子力学は、電子だけのための力学ではないんだよ。 へぇ、電子以外にもあてはまるのね、世界が拡がった感じがする。
へぇ、電子以外にもあてはまるのね、世界が拡がった感じがする。 量子とは、波と粒の両方の性質を持つような小さいもの、と考えてもらったらいいと思うよ。
具体的には、素粒子や素粒子が数個集まったものなどだね。
量子とは、波と粒の両方の性質を持つような小さいもの、と考えてもらったらいいと思うよ。
具体的には、素粒子や素粒子が数個集まったものなどだね。 波の性質を持つ粒か~。
波の性質を持つ粒か~。 もちろん答えは「はい」です。
もちろん答えは「はい」です。 ありゃ。じゃあ、さっきのは愚問だったわけね。
ありゃ。じゃあ、さっきのは愚問だったわけね。 大きなものに量子力学を適用しても結果は同じになるけど、そんな面倒なこと誰もしないね。
大きなものに量子力学を適用しても結果は同じになるけど、そんな面倒なこと誰もしないね。 でも、すべての物質は波の性質を持つ、と言われてもピンとこないわ。
でも、すべての物質は波の性質を持つ、と言われてもピンとこないわ。 確かにそうなんですよ。
確かにそうなんですよ。 スケールが大きくなると波としての性質が現れにくくなるから、量子らしさは見えにくくなるね。
スケールが大きくなると波としての性質が現れにくくなるから、量子らしさは見えにくくなるね。 なるほどね。
なるほどね。 大きい方の境界は、粒だと思っていたものが、波特有の干渉の性質があるかどうか、で判断できる。過去にあいまいな状態だった領域が、実験と理論が合っていって少しずつ狭まっていったという経緯があるよ。
大きい方の境界は、粒だと思っていたものが、波特有の干渉の性質があるかどうか、で判断できる。過去にあいまいな状態だった領域が、実験と理論が合っていって少しずつ狭まっていったという経緯があるよ。 へぇ、どんな実験?
へぇ、どんな実験? 二重スリット実験で、干渉縞が見えるかどうか、という実験です。
二重スリット実験で、干渉縞が見えるかどうか、という実験です。 じゃあ、陽子が波の性質を持つかどうか、実験で確かめたことはあるの?
じゃあ、陽子が波の性質を持つかどうか、実験で確かめたことはあるの? うーん。
うーん。 KEKは陽子の加速器も扱っているんじゃなかったっけ?
KEKは陽子の加速器も扱っているんじゃなかったっけ? もちろん、いまは東海村のJ-PARCで陽子を実験に使っていますけど、J-PARCはその名の通り「大強度陽子加速器施設」で、扱うのはエネルギーの高い陽子です。
もちろん、いまは東海村のJ-PARCで陽子を実験に使っていますけど、J-PARCはその名の通り「大強度陽子加速器施設」で、扱うのはエネルギーの高い陽子です。 ふ~ん、そんなものなのね。
ふ~ん、そんなものなのね。 ですが、陽子は非常に小さくて、問題なく量子力学が使える領域です。
ですが、陽子は非常に小さくて、問題なく量子力学が使える領域です。 はぁ、安心して使います。
はぁ、安心して使います。 それをこれから説明しますよ。
それをこれから説明しますよ。 もちろん。
もちろん。 よかった。じゃ、これで行きましょう。
よかった。じゃ、これで行きましょう。 ところで、演算子ってなんなの?
ところで、演算子ってなんなの? +とか-とか×とか÷とか、のことにゃ。
+とか-とか×とか÷とか、のことにゃ。 それは算術演算子だね。一口に演算子と言ってもいろいろあるんだよね。
それは算術演算子だね。一口に演算子と言ってもいろいろあるんだよね。 <とか=とか and とか or とかのこともあるニャ。
<とか=とか and とか or とかのこともあるニャ。 それはプログラミングでも使われる演算子だね。いままで出てきたのは数学的な演算子だよ。
それはプログラミングでも使われる演算子だね。いままで出てきたのは数学的な演算子だよ。 ふうん。アクションを示しているわけね。
ふうん。アクションを示しているわけね。 例えば、こんな感じ。
例えば、こんな感じ。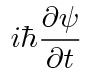
 なるほど。掛け算みたいで掛け算ではない。
なるほど。掛け算みたいで掛け算ではない。 物理量を表す0じゃない実数です。
物理量を表す0じゃない実数です。 ふうん。
ふうん。 そうとも言えますね。
そうとも言えますね。 「独立な変数をもつ」2つの関数ってどういう意味?
「独立な変数をもつ」2つの関数ってどういう意味? 例えば、1の式が分子の重心運動の話、2の式が分子の回転運動の話だと思ってください。
例えば、1の式が分子の重心運動の話、2の式が分子の回転運動の話だと思ってください。 長さと角度は互いに独立しているという意味かなぁ。
長さと角度は互いに独立しているという意味かなぁ。 そう、この変数の違いがポイントです。
そう、この変数の違いがポイントです。 はい、成りたちます。
はい、成りたちます。 じゃあ、1の式には(関数2)をかけて、2の式には(関数1)をかけましょう。
じゃあ、1の式には(関数2)をかけて、2の式には(関数1)をかけましょう。 関数に関数をかけるの?
関数に関数をかけるの? そうです。
そうです。 え?何か言いました?
え?何か言いました? いえ、何も。
いえ、何も。 ですよね。
ですよね。 この2つの式の左辺同士を足し合わせたものは、右辺同士を足し合わせたものと等しい、
この2つの式の左辺同士を足し合わせたものは、右辺同士を足し合わせたものと等しい、 元の式と同じ形になったにゃ~。
元の式と同じ形になったにゃ~。 そうですね。
そうですね。 その通りです。
その通りです。 ほんとだニャ~。
ほんとだニャ~。 つまり、固有値のたし算 E1+E2+E3に対応する波動関数は
つまり、固有値のたし算 E1+E2+E3に対応する波動関数は はい。
はい。