北村 源次郎：野趣あふれる美猫。上田城で母と運命の出会いを果たし、北村家の猫となったことから、真田信繁の幼名をとって源次郎と名付けられた。
十八番は即興ピアノ曲「猫が踏んじゃった」。
母上：源次郎の母。文系だが、素粒子とスピンに興味がある。昆虫・植物が大好きで、KEK構内で撮った珍しい虫の写真を持ち歩く。
プロフィールはKEKのひと「山を旅して世界を知った 北村節子さん」に詳しい。
【KEKエッセイ #1】「天才はおもいがけなくやってくる」
【KEKエッセイ #7】「メンデレーエフの日本の孫」
前回までのお話:
クンクン
クンクンクン
何者ニャ？
わたし？
シュレディンガー家に出入りしてる猫。名前はまだにゃいの。
もしかして…逃げてきたの？
まぁ、そんなとこかにゃ。
あら、源次郎。お友だち？
はじめまして。
え？シュレディンガー家から逃げてきた？
実験台にされそうになったってこと？
ちゃんと逃げるからご心配なく。それに、エルヴィン先生は猫が苦手だから、私を捕まえて箱に入れたりしないわ。
そうなのか。シュレディンガーさんちの猫は一枚上手だニャ。
大変だったのね。ゆっくりしていってね。
今日はシュレディンガー方程式を分からせての日なのよ。
うちの先生が何をやっていたか、わたしもよく知らにゃいの。連れてってほしいにゃ。
じゃあ、一緒に出発ニャ！
愛媛県松山市出身。専門は、物性物理学。幼いころから磁石の不思議に魅せられて、かれこれ半世紀、今も磁石に関連した研究を続けている。
【KEKエッセイ #10】「百万聞は一見に如かず～光を作る工場」
今日はシュレディンガーさんちの猫も連れてきちゃいました。名付けてシュレ子ちゃんです。
そう。シュレディンガーは電子の「波としての性質を表す式」を考えたんだ。
電子が粒子であると同時に波の性質をもつから、ですね？
そのとおり。
その「波動関数」って何なの？
電子の状態を表す量と言ったらいいかな。
えっと、複素数って虚数と何が違うんでしたっけ？
二乗すると負の数になるのが虚数、そうでない普通の数が実数だけど、複素数は実数と虚数を足し合わせた数だね。
どうして電子の状態を表すのに、複素数が必要なの？
鋭い質問だね。
何か物理的な意味があるのかと思ったのに、それだけ？
「波動関数」が何を表しているのかということは、当時も、実は今も大問題なんだ。
シュレディンガー自身も物理的な意味は説明できなかったようなんだよね。
うちの先生、式を作ったのに、その答えの意味は説明できなかったってこと？
残念だけど、そうみたいだよ。
それなのに、シュレディンガーの式が認められたのはどうしてなの？
シュレーディンガー方程式を解くことによって、原子内の電子状態などが明らかにされ、数多くの実験結果を見事に説明することができたからなんだ。
ふぅん。
一言でいうと、エネルギーに関する式だね。物質の波としてのエネルギーが粒子としてのエネルギーに等しいとおくと、「シュレディンガーの」波動方程式のできあがりだよ。
式の成り立ちは明快なのね。
そうそう。
奇妙な考え？
その奇妙な考えっていうのはね、シュレディンガー方程式が解けたとして、位置と時刻を指定すると波動関数の値が出てくるよね。
波動関数の大きさの二乗って？
複素数の大きさはどうやって求めるか考えてみようか。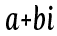
この複素数の大きさを求めるには、こういう計算をするよ。
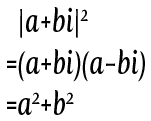複素数平面と三角形を使って図に表すと、こうなる。
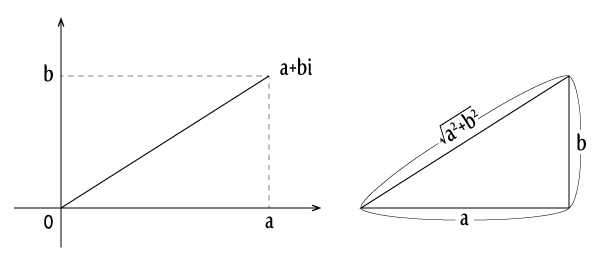この計算ででてきたのは大きさの二乗だね。
だから、複素数の大きさを考えるとき、二乗は自然に出てくる、と言ってもいいかもしれない。
なぜ二乗が出てくるのかなと思ってたのよ。ボルンは大きさに着目したのね。
それでは思考実験として、1個の電子を観測する場合を考えよう。
テニスの試合の解説で出てくる打球の痕跡を集めた画像みたい。
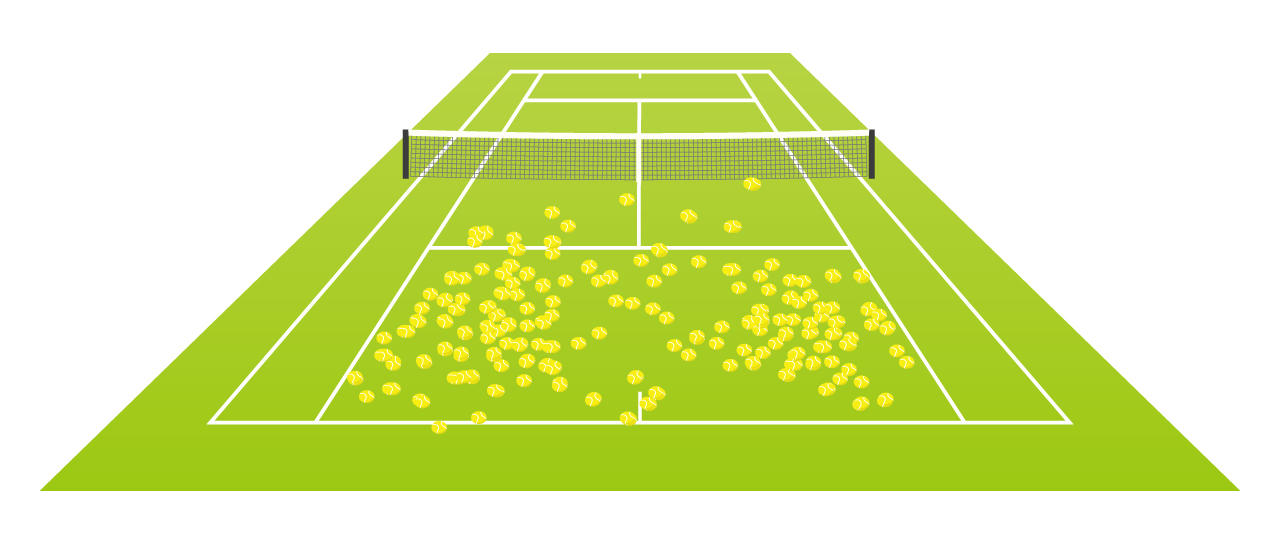
この分布は、どこで電子を見つけることができるかという確率分布であると考えてもいい。
へぇ。計算と実験が合うなら本当なんでしょうけど、なんだか、分かったような分からないような話ね。
電場のエネルギーが電場の二乗に比例するという関係があって、その類推じゃないかという考えがあります。
ふ～ん。
電子波を表す波動関数から、電子を粒子的に見出す確率を求めることができるということなんだ。
「使ってみたら合っていた」というのは、「物理学は理詰めで進められる、演繹的な学問」という私のイメージと、どうも食い違うんだよね。
物理学では、いくら美しい理論でもその理論が予測する結果が実験で確かめられるまで、その理論が正しい理論であるとは認知されないんだ。
なるほど。
そうだね。
うわぁ、何だかたくさん並んでる…。
降水確率を地図に描いたものを見たことあるかな？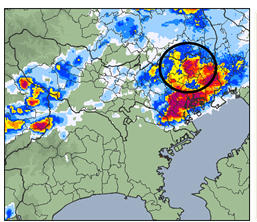
こんなかたちで分布するでしょう、という予想図みたいなものね。
ここで最初の「殻の中の電子の軌道」の話に戻るんだけど、上の表をよく見ると、一番上のK殻のところには1sと書いてあるよね。
これは、K殻には1s軌道があるという意味なんだ。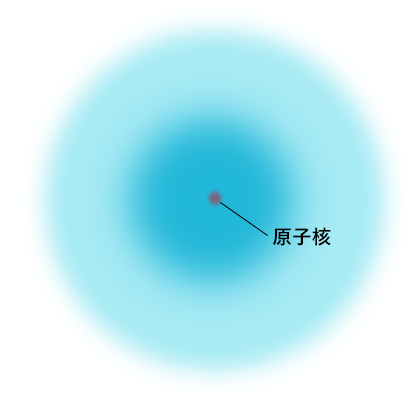
ああ、あのモアッとした図のことね。上の図は同じ値の点をつないだ等高線みたいなものってことか。
電子が1つでもこのような軌道をとる可能性があるということなんだ。
同じ一つの電子でも、あらわれ方は幾通りもあって変幻自在なのね。
その通り。L殻はK殻を包みこむ大きさで、その中にはs軌道もあるしp軌道もある。
例えば…、ゆで卵の黄身の大きさがK殻で、白身の大きさがL殻だとしますよね。
それはちょっと違ってて、L殻の電子の軌道は黄身の部分にもあるよ。
そうなんだ。もうどこにいてもおかしくないんだ。びっくり。
そういうこと。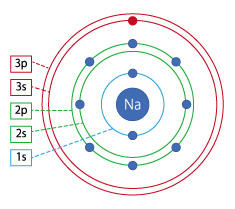
なるほどね。
そう。だから電子たちは基本的に原子核に近いほうの席から埋めていくんだね。
基底状態が好きすぎて、一つの席に殺到したりしないの？
おっ、源ちゃん。いいところに気がつきました。
えっ？誰だろう？
じゃあ、今日のわたスピはこの辺にして、この後はシュレ子ちゃんの身の上話でも聞かせてもらおうかな。
賛成！
前回までのお話一覧:
スピンオフコラム：私にスピンをわからせて! スピンオフコラム ～ KEKの2つの研究所 ～
