北村 源次郎：野趣あふれる美猫。上田城で母と運命の出会いを果たし、北村家の猫となったことから、真田信繁の幼名をとって源次郎と名付けられた。
十八番は即興ピアノ曲「猫が踏んじゃった」。
シュレ子：第4回転から登場、ヨーロッパからやってきた謎の猫。
母上：源次郎の母。文系だが、素粒子とスピンに興味がある。昆虫・植物が大好きで、KEK構内で撮った珍しい虫の写真を持ち歩く。
プロフィールはKEKのひと「山を旅して世界を知った 北村節子さん」に詳しい。
【KEKエッセイ #1】「天才はおもいがけなくやってくる」
【KEKエッセイ #7】「メンデレーエフの日本の孫」
【KEKエッセイ #15】「原爆投下。チャーチルは、ママの実家を頼った？」
前回までのお話：
あらすじ：
スピンとは何かを知る旅に出た源次郎と母上は、スピンの存在を決定づけた一つの実験に出会う。しかし、「スピンって何？」の答えの前に、原子やら軌道やらほどほどの予備知識を携えつつ専門用語の波に抗う必要があることを知る。しかしめげずに進むふたり。猫の シュレ子も加わって、図らずも量子力学の歴史をたどり、「それってスピンじゃなければ説明できないじゃない！」と叫ぶ寸前のところまで来ている。
そういえば、シュレ子ちゃん、逃げてきたんだっけ？
何かあったのかニャ？
逃げてきたっていうのは本当は違うにゃ。エルヴィン先生がね、代わりに行ってきてほしいって。
え？どういうこと？
本当は前回って、エルヴィン・シュレディンガー先生が出演するべき回だったじゃない。シュレディンガー方程式の巻なんだから。
まぁ…確かに。
シュレディンガーの猫：シュレディンガーが「量子力学的な重ね合わせ状態が存在するなら、人間の感覚で感知できるスケールの重ね合わせ状態が実現する例」として挙げた有名な思考実験に出てくる仮想の猫、あるいは思考実験そのものを指す。
密封できる箱の中に原子核の崩壊を引き金にして猛毒が放出する仕組みを作り、猫を入れておく。一定時間のうちに原子核が崩壊すれば猫は死ぬ。崩壊しなければ猫は生きている。
原子核の崩壊はその確率だけが分かっており、観測するまではどちらか分からないので、量子力学では崩壊と非崩壊の2つの状態が重ねあわせになっているという。原子核が崩壊するかしないかというミクロな現象が、猫の生死というマクロな現象に見事に投影されている。
だけど、「今の世の中ではシュレディンガー方程式よりも『シュレディンガーの猫』の方が有名になっているようだ。猫を危険にさらす可能性のある装置を考えたのは自分だけど、実際にはシュレディンガー家に出入りしている猫は虐待なんてされてないってことを証明してきてくれないか」って相談されたのにゃ～。
あれ？シュレ子ちゃん、シュレディンガーさんは猫が苦手だって言ってなかった？
そうにゃんです。だけど、遠くから話しかけてきて…。
わたし、エルヴィン先生のこと嫌いじゃないから、引き受けてみたというわけにゃの。
へぇ、そうだったの。
エルヴィン先生は、生命の不思議について考えてるって聞いたにゃ。本も書いてたみたい。
そういえば、シュレディンガーには "What is life?" というタイトルの著書があるって聞いたことあるニャ。
あら、源次郎、物知りね。
"What is life?" というのは、物構研の構造生物学研究センターのテーマと同じだね。
シュレディンガーは量子力学を突き詰めた後、「生命とは何か」を考え、生細胞を物理的に捉えることに挑戦した。特に遺伝の仕組みは飛び飛びの状態を表す量子論で説明できると考えたらしい。分子生物学のはしりだね。
生命のことが気になり始めた物理学者が、思考実験の箱の中にも命あるものを持ち込んでしまうのは分からないでもないわね。
先生が考えているとき、たまたまわたしが目につくところにいたのかもしれないにゃ～。
愛媛県松山市出身。専門は、物性物理学。幼いころから磁石の不思議に魅せられて、かれこれ半世紀、今も磁石に関連した研究を続けている。
【KEKエッセイ #10】「百万聞は一見に如かず～光を作る工場」
【KEKエッセイ #19】「相転移～景色が突然変わるとき」
そもそも、前回シュレディンガーが出てきたのはどうしてでしたっけ？
私たちは銀原子について考えていたよね、シュテルンとゲルラッハの実験の謎を解くために。
ふんふん、K殻、L殻…ってやつね。
だけど、電子の軌道、つまり電子が存在する可能性がある場所を詳しく調べると、実はもっと小さい単位の軌道の組み合わせだということが分かったんだ。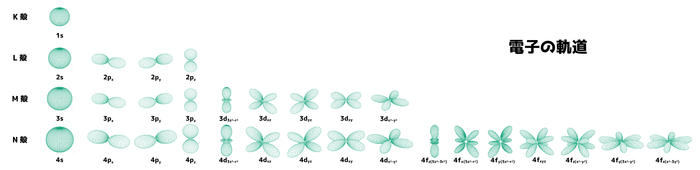
そっか、シュレディンガー方程式があったから、軌道の詳細まで分かるようになったのね。
そう。その小さい単位の軌道というのを、さっきの図に当てはめてみると…こうなる。
うわっ！
つまり、シュレディンガー方程式によれば、電子の軌道は最大2つの電子が入る小さい軌道の組み合わせ、ということになるんだ。
なるほど、よく見ると、一本の線上には丸は2つしか乗ってないわね。
母上、スイスからヴォルフガング・パウリさんって人が来たニャ。
パウリさん？
こんにちは。前の前の回にボーアがここに来たそうで。彼は年上なんですが、元同僚なんですよ。
あらそうなんですか。
ええ。
あら嬉しいわ。
1つの軌道には最大2つの電子が入るという話をされていましたね。
席が2つしかないから…、じゃあ答えにならないわね。実際に椅子があるわけじゃないものね。
じゃあ、これを見てください。あり得ないけど、軌道に入ろうとする電子のための看板だと思ってもらえるとありがたい。
ふんふん、1つの軌道には電子は2つまでね。さっきの図の通りね。
でもこれじゃ、不十分なんです。結果として2つなんだけど、なぜ2つなのかの理由が分からない。
単に、同じ「状態」のものは複数入れません、というルールだと考えるとスッキリするんです。
2つの電子には違うところがあって、お互いに違うもの同士だから2つ入れるってことかなぁ。
そういえば、電子には「個性がない」って聞いたことがあるニャ。同じ電子だけど「状態」が違うの？
そう。全く同じだと思っていた同一軌道上の電子2つに実は違いがあって、「全く同じ状態の電子は同じ軌道に共存しない」というルールがあると考えると、とてもシンプルに説明ができる。
「パウリの排他律」と言われているものですね。
同じ軌道にいる電子には2つの「状態」があるってことだニャ。
そう、電子には今まで知られていなかった「状態の違い」があることが様々な実験で明らかになって、私たちはそれを「新しい自由度」って呼んだんだ。
自由度？
例えば、オセロの石は全部同じだけど、黒い面と白い面があるよね。黒か白かは変化する余地がある。それを自由度って呼ぶんだよ。
なるほど。
もちろん。
ふ〜ん。最後に発見された自由度か…。
そう、「新しい自由度」とはいわゆるスピンのことを指している。
じゃあ、電子が一つの席に殺到しないのは、電子にスピンがあって排他律に従ってるからニャンだね！
その通り。
ん？他にスピンを発見した人がいるのね？
いや、だれか特定の人物がスピンを発見したというわけではないんだよ。
へぇ！そうなのね。
スピンという概念は、量子力学がいまの形に近くなったころに生まれたものだけど、みんなの実験や思考を重ねた上での議論の中で、電子には「新しい自由度」つまりこれまで知られていない性質があるということが共通認識になっていった。
どうりで「スピンの発見者」がでてこないわけね。
アインシュタインが単独で「相対性理論」を作り上げたのとは対照的ですね。
初めは「スピン」＝自転という考え方もあって、私は反対だった。
だから私が混乱したのよね。何が回ってるの？って。
いやいや、こんなキャッチーな名前じゃなければ、北村さんもここまで気にならなかったんじゃないのかなぁ。
僕はパウリさんの背景の割れてる皿とかカップは何なのか気になるニャ～。
自分で説明するのも何なんだけど…
「パウリ効果」ってにゃあに？
僕が近くにいると装置やら何やらが壊れると言われていて、
パウリの排他律は厳しーっ！
原子の構造について一通り分かったところで、シュテルンとゲルラッハの実験、銀原子に戻りましょう。
そうだった、銀原子の話をしていたんでした。
まず、実験者のつもりになって考えてみようか。
機械仕掛けのダーツみたいなもんよね？たまに外れるかもしれないけど、真ん中に集中すると思う。
そうだよね。当時の科学者の予想もそうだった。
だけど、実際にはまっすぐ進む原子はほとんどない…って話にゃのよね…？
そう、銀原子が進んでいる空間には磁場があって、銀原子はS極に向かうものとN極に向かうものの二手に分かれた。
そうだったね。じゃあ、銀原子の磁気モーメントについて詳しく考えてみよう。
銀原子には電子で満杯になった複数の殻と一番外側の殻に1個の電子があるね。
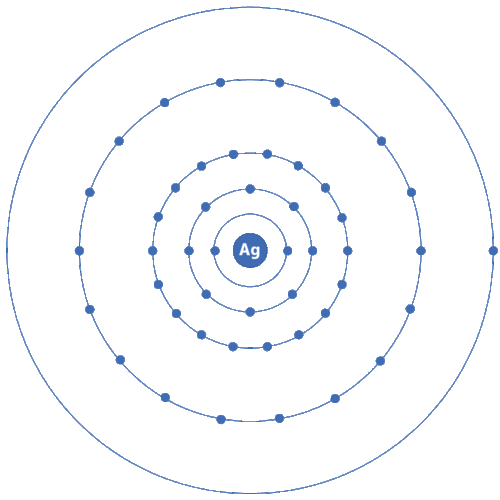
電子で満席の殻は、軌道磁気モーメントが打ち消し合ってゼロだニャ。
そのとおり。
そういえば、前々回わたスピ3で、1s軌道の話が途中になっていた気がする。
そうそう、確か s軌道のかたちは真ん丸だから、と言っていたような…。
源次郎くん、冴えてるねぇ。
そうね、一つの円周上を回っていたらゼロじゃないだろうけど、ありとあらゆるところに存在するとしたら、平均するとゼロになっちゃうんでしょ？
だとすると、銀原子の一番外にある電子は軌道磁気モーメントがゼロだニャ。
源次郎、シュレ子ちゃんの前でいいとこ見せたわね。
そうすると、銀原子全体の軌道磁気モーメントはゼロだということが分かったね。
原子の電荷はゼロで、磁気モーメントのうち、軌道磁気モーメントはゼロだから…
なるほど、ここでスピンが浮上してくるわけね。
スピンに思い当たりましたね。
スピンが答えかどうかは分からないけど、スピンで説明できるかどうか確かめるってことだニャ。
そうだよ。まずは内側から。
ヒントをもう一つちょうだい。
はい、打ち消し合いますよ。
じゃあ、電子が2つ入っている軌道はプラスマイナスゼロ！
ご名答！
ってことは？
そういうことになりますね。
ちっぽけな電子がたった1つで、重い銀原子の進行方向を曲げていたなんて！
当時の物理学者も北村さんと同じように随分と悩んだようですよ。
へーぇ。そうなんだ。
例えば、原子の芯という考えがあったんだ。
にゃるほど。いろいろ考えたのね～。
でも、この芯の磁気モーメントでは、「実際に実験で求められる磁気モーメントの大きさ」と「ある理論に基づいて計算された磁気モーメントの大きさ」が合わなかった。
こうなるだろうと頭で考えたのと、手を動かして実験や計算をしてみるのとでは、違いますよってことかニャ。
にゃ～るほど。だから、原子の芯を考えた人たちも、スピンの存在を認めたってわけね。
そういうこと。
まっすぐでもなく、上だけでも下だけでも斜めでもなく、全ての原子は上か下のどちらかに行くのね。
そう、表か裏か、プラスかマイナスか、左か右か、みたいに、二者択一だってところがポイントなんだ。
電子がスピンという性質を持つということは、今までのお話でだいぶ納得できた気がする。
わたスピ基礎編、卒業だね。
ありがとうございます！
ありますよ。たくさん。
ふ～ん。陽子のスピンも知りたいな。
物構研で扱うスピンはほとんどが電子のスピンなんですよね。前回までのお話一覧：
スピンオフコラム：私にスピンをわからせて! スピンオフコラム ～ KEKの2つの研究所 ～
