北村 源次郎：野趣あふれる美猫。上田城で母と運命の出会いを果たし、北村家の猫となったことから、真田信繁の幼名をとって源次郎と名付けられた。
十八番は即興ピアノ曲「猫が踏んじゃった」。
シュレ子：第4回転から登場、ヨーロッパからやってきた謎の猫。どうやらシュレディンガー家から来たらしい。
母上：源次郎の母。文系だが、素粒子とスピンに興味がある。昆虫・植物が大好きで、KEK構内で撮った珍しい虫の写真を持ち歩く。
プロフィールはKEKのひと「山を旅して世界を知った 北村節子さん」に詳しい。
【KEKエッセイ #1】「天才はおもいがけなくやってくる」
【KEKエッセイ #7】「メンデレーエフの日本の孫」
【KEKエッセイ #15】「原爆投下。チャーチルは、ママの実家を頼った？」
【KEKエッセイ #24】偉大な博士の「最後のイチジクの葉」
前回までのお話：
あらすじ：
源次郎と母上のスピンとは何かを知る旅に、猫の シュレ子も同行することになった。
様々な実験での原子のふるまいを説明するには、電子のスピンという概念が必要だと分かり始めた母上は、ついに指南役の村上先生からわたスピ基礎編卒業を認定された。
しかし、お祝いムードもつかの間、母上には次の疑問が沸き起こるのだった。
前回村上先生が言ってたニャ～。
「物構研で扱うスピンはほとんどが電子のスピン」だって。
「ぶっこうけん」って何？
あ、シュレ子ちゃんに教えてなかったね。KEKに2つある研究所のうちのひとつニャんだ。
へぇ、KEKの中に2つも研究所があるにゃんて。
「ぶっこうけん」って何の略？
「物質構造科学研究所」の略ニャ。
にゃ～るほど、分かった。
「物質」は原子でできている。原子は原子核と電子でできている。
原子核はなかなか壊れないにゃ。
放射性元素は崩壊するニャ。
まぁ、そうだけど、放射性元素はそんなに多くないし、原子核に対して一番外側にある電子は割と自由に動けるから、電子の動きが気になるというのは分かる気がするにゃ～。
なになに？ 何が割と自由に動けるって？
あら、源ちゃんのお母さん。
電子のことを話してたにゃ。
今日はね、電子以外のスピンの話を聞くのよ。
じゃあ、物構研で扱うスピンとちょっと違うんじゃにゃいの？
そう。だから今日はKEKのもうひとつの研究所「素粒子原子核研究所」の先生を呼ぼうと思ってるニャ！
にゃんと！
でもきっと村上先生も来るニャ。
村上先生は、担任の先生みたいな感じかしらね。
愛媛県松山市出身。専門は、物性物理学。幼いころから磁石の不思議に魅せられて、かれこれ半世紀、今も磁石に関連した研究を続けている。
物構研に新設された量子ビーム連携研究センター（CIQuS）の専任教員。
【KEKエッセイ #10】「百万聞は一見に如かず～光を作る工場」
【KEKエッセイ #19】「相転移～景色が突然変わるとき」
千葉県松戸市出身の理論物理学者。2020年3月まで、KEK 素粒子物理学研究所 理論センターに所属、同年4月から長崎総合科学大学 教授。
高エネルギー重イオン衝突や高エネルギーのハドロン散乱などの極限的な状況の物理に興味を持って研究している。
板倉さん、よろしくお願いします。
こちらこそよろしくお願いします。
電子にスピンがあるということの経緯はガッテンしたところなんですが、陽子のスピンを調べようと思ったきっかけはなんでしょう？
電子にスピンがあったと聞くと、他の粒子にあるのかどうか調べたくなるという好奇心じゃないですかねぇ。
あ、なるほど。
電子のスピンは数式で表すことができるんですね。その式が、例えば陽子に対しても使えるか、という興味もあったのだと思います。
電子で分かったことが一般化できるか調べたかったということね。
ラザフォードによって「陽子」という概念が提案されたのが1920年ごろ、スピンの概念が生まれる5年ほど前だった。
「1920年ごろ」というのはどうしてなの？
これが、諸説あるんですよ。
そうかもしれません。
陽子のスピンの発見までにはたくさんの実験が行われるんですが、
気体ですか、何だろう？？？
う～ん…
じゃあ、ここでちょっと復習。
内側の電子の影響はすべて打ち消しあっていて、一番外側の電子1個のスピンだけが影響して原子が曲がったんでした。
そうそう。
じゃあ、銀原子の電子が1つ少ない原子だったらいいのかニャ？
でもそれだと中性子の影響は？
そうですね。原子番号の大きな原子だと話が複雑になるから、
水素にゃ。水素の原子核は陽子だけにゃもん。
水素原子は電子も1つじゃない？ 電子は2つ組じゃないと打ち消し合えないと思うけど…。
シュレ子ちゃん、正解。水素です。
なるほど、それなら電子スピンの影響は無視できるわね。
水素分子は実際には陽子2つの周りに電子2つがあるようなかたちになっているんですよね。
この水素分子の絵は、物構研の「一家に1枚 水素ポスター」から借りてきたんだけど、ちゃんと距離を計算して描かれているそうだよ。
2つの原子がくっついちゃってるニャ。
このとき2つの原子は共有結合をしています。
共有結合は、化学で習ったわ。
不対電子同士が組になると強い結合を示す、と習ったよね。こんな記号で。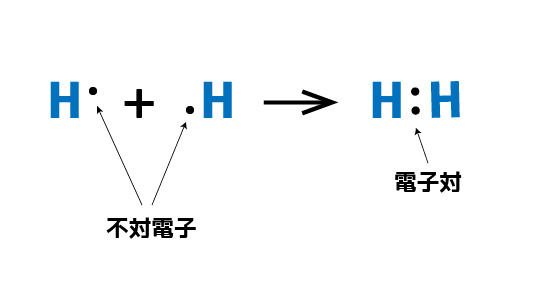
へぇ。
水素原子になったつもりで考えてみよう。
私は登山が好きだけど、わざわざ登る理由もないからすべり台かな。
そうだね。一般にはエネルギーが低くなる方向の変化の方が起こりやすい。
エネルギーが低くて安定している軌道のときは、強く結合しているってことね。
じゃあ、このグラフを見てみましょう。
北村さんの質問は、陽子同士が近づいたときに反発し合わないか、ということでしたね。
さっきみたいに山に例えたら、急な斜面を登っているようなものね。
そう。
緩やかな斜面を下っているみたい。
結合性軌道の場合、それぞれが水素原子でいたときよりもエネルギーが低くなるんだ。
どうしてこんな凹みができるの？
電子が結合性軌道を形成するときには、近づけば近づくほど結合が強くなる一方で、陽子同士の反発力も大きくなるからなんだ。
なるほど、その距離が、遠すぎず近すぎず、2つの力のバランスがとれている近さってことね。
こういう凹みのことを「ポテンシャルの井戸」って言うんだよ。
勢いで、井戸を飛び超えて Re より近づいてしまうことってないのかしら？
もし Re よりも近づくことができれば、2つの陽子が反応して核融合が起こってしまいます。
えっ？！ 核融合！？
仮にそんなことが起これば、水素の原子核が変化してしまうんだけど、それには非常に高いエネルギーが必要なんだ。
そっか、そのぐらいハードルが高ければ容易には起こらないわね。あーびっくりした。
そう。人工的に核融合を起こすことは非常に困難だということも分かりますよね。
ちなみに、電子が反結合性軌道をとるとき水素のイメージはこうなるよ。
ふーん。2つの電子雲が避け合っている感じね。
孤立電子対が2つあるように見えるけど、これで一つの電子軌道なんだよ。
それで水素分子を使ってどんな実験をしたの？
1927年ころ、ドイツのフリードリッヒ・フントが、デンマーク コペンハーゲン大学のボーア研究所にいて、陽子のスピンの存在を予測していた。
比熱？
比熱とは、
熱しにくく冷めにくい物質ほど、比熱が大きい、というやつね。
はい。陽子スピンに関係して登場するのは、水素ガス、つまり水素分子の集団に熱を与えて、どのくらい温度が上がるかを測る、という比熱の実験なんです。
え、それってちょっとアナログな印象。
全くその通り。
え～、どんなふうに？ ちょっと想像つかないな。
量子力学が生まれる前、19世紀には、ある条件のときに気体の状態を表す式が成り立つことが知られていたんです。
気体の状態と言うと？
そうそう。気体の体積と温度と圧力と量が満たす式で、気体の状態方程式と言います。
聞いたことあるわ。
現実の気体は一筋縄じゃいかなくてその式だけで表すことはできないけど、理想的な条件ならその式が成り立つ、と言ったらいいかな。
現実にはいろんなことがあるけど、大筋では合ってる式ってことかしら。
はい。
えーっと…
母上、元素の周期表に書いてある質量は、1モルあたりの質量だって言ってたニャ。
もしかして、アボガドロさんじゃにゃい？
そうそう。原子や分子をアボガドロ定数個集めたものを1モルと言うんだね。
さっき私が「アナログ」といった量と、超デジタルな量子の話が結びつくのね。
じゃあ細かい方から行きましょう。
質問が急ね。
そうですね。
えっ？なんで？
話をシンプルにするために、容器に閉じ込めた気体を考えますよ。つまり、気体の体積と量は一定です。
分かった。暑いときほど気体分子が速く動き回ってるということね。
そうです。例えば25℃のとき水素分子の平均速度はジェット機の8倍くらいと言われています。
へぇ！
気体分子の運動エネルギーの平均値が、気体の温度に比例するという話は高校の物理の教科書にも書いてあるので、もっと詳しく知りたかったら勉強してみてくださいね。19世紀には既に発展していた気体分子運動論です。
気体の状態方程式が役に立つというのも分かりました。
さて、分子の運動エネルギーを全て足し合わせたものを、気体の「内部エネルギー」と呼びます。運動エネルギーの平均値が温度に比例するなら、これも温度に比例しますね？
はい。
先ほど、ある条件でだけ成り立つ状態方程式という話をしたんですが、いちいちそう言うのは面倒なので名前がついてます。
その条件を満たすような気体を「理想気体」と呼びます。
この横軸の「絶対温度」というのは？
熱力学で扱う温度は絶対温度といって、私たちが日常使う摂氏とは273.15℃ずれています。
例えば、25℃は298.15Kですね。
300℃近くずれてるのね。どうしてこんな温度を使うの？
摂氏というのは、18世紀の天文学者 アンダーシュ・セルシウスのことなんだけど、セルシウスは水の凝固点を温度の基準と考えた。
それが-273.15℃だった、ということね。
そう。絶対温度を提唱した物理学者ウィリアム・トムソンがケルヴィン卿と呼ばれていたので、単位をケルビン[K]とし、セルシウス温度の刻みはそのまま使って、273.15℃シフトしたということなんだ。
温度の単位は人の名前に由来してるのが多いのねぇ。
では比熱に戻りましょう。
傾き！
ということは、これは理想気体では定数になります。
え？定数？
理想気体の場合、分子がいくつの原子でできているか、で異なります。
母上、高校の物理の教科書、借りてきたニャ。
おっ、源ちゃん、サンキュー。
| ヘリウム He | 12.5 J/(mol・K) |
| アルゴン Ar | 12.5 J/(mol・K) |
| 水素 H2 | 20.4 J/(mol・K) |
| 一酸化炭素 CO | 20.8 J/(mol・K) |
分子式を見たら原子の数が分かるにゃ。
そうね。
そう思いますよねぇ。
ところが、多原子分子になると話が違ってきます。
多原子分子っていうのは、2つ以上の原子でできた分子ってことね。
そう。例えば水素や一酸化炭素のような二原子分子なら、重心移動に加えて分子が回転する。
原子の数というより、形の違いが問題ってこと？
それは形が変わったことにならないから、考えなくていいんです。
ふ～ん。
単原子分子に比べて、二原子分子は回転できる分だけ自由度が大きい、つまり動きの種類が増える、ということですよ。
確かに。丸い分子より、ダンベル型分子の方が、余分な動きをしそうだわ。
単原子分子は縦横高さで運動の自由度は3になります。
理容室のサインポールみたいにくるくる回るのは、さっきの自転とおなじだから、入りませんね？
はい、入りません。
じゃあ、えーっと、緯度と経度で2つ！
そうですね。
ちょっと計算してみる。電卓、電卓。
いまのは25℃での値でしたね。
へーっ！
そうなんです。重心の運動エネルギーが連続的に変化するのに対して、回転のエネルギーはとびとびの値しか取れません。回転運動は量子力学の領域なのです。
このグラフ、もっと上がありそう。
おっ、鋭いですね。実はもう一段階あるんです。
ぶるぶるぶる、って震える振動？
確かにそうですね。
振動と言っても分子ごと震えるんじゃないのね。
原子間の距離が伸び縮みして形状自体がかわるような振動ですね。
なるほど。
20世紀になって原子のモデルが明らかになってくると、それまで考えられてきた気体分子の運動を、原子核と電子に分けて考えるようになりました。
理想と現実の差を埋めようと考えたのね。
そう。
ふんふん、やっとフントさんに戻ってきました。
いえ、水素分子の結合性軌道に入っている電子が持つ運動エネルギーとポテンシャルエネルギーの和です。
それはどうして？
結合性軌道から反結合性軌道までのエネルギー間隔が大きいので、ほぼ全ての電子が結合性軌道にあり、比熱への寄与はとても少ないからです。
そうか、振動のエネルギーも電子のエネルギーも冬眠中だ、と。ところが何かが動いている。それが何かを突き止めようとした、ということですね？
そうですね。低温なら影響するのは、重心運動と回転運動と、その他のエネルギーだけ。
回転のエネルギーか。
叩きこまれたんですか。
水素分子の回転エネルギーは、J という数が大きくなると大きくなる、という意味かしら。
回転に関する量子力学計算からよく分かっていましたし、実際に分光実験でも確かめられていました。
パウリは実験はしないって聞いたから、他の人の実験結果を見て予想したのね。
おそらくそうでしょうね。
この場合は回転エネルギーに関係する量子数だから、回転量子数というんだね。
どうして J なの？
Ｊは量子力学で角運動量を表すときによく使う記号ですね。
あ、そうなんだ。何かの頭文字かと思ったので。
慣例的によく使う文字が決まっているんですよね。
初めて見る人には分かりにくいかもしれませんね。
えっ！？
どうしました？
そんなこと、聞いてませんでした。パウリの排他律に従わないものがあるなんて。
いや、前回説明が足りなかったかもしれないけど、パウリは電子について考えて排他律を見つけたわけで…
母上…
この後どうなったかはご想像にお任せします。
今回はここまでなのにゃ～。
前回までのお話一覧：
スピンオフコラム：私にスピンをわからせて! スピンオフコラム ～ KEKの2つの研究所 ～
