北村 源次郎：野趣あふれる美猫。上田城で母と運命の出会いを果たし、北村家の猫となったことから、真田信繁の幼名をとって源次郎と名付けられた。 十八番は即興ピアノ曲「猫が踏んじゃった」。
シュレ子：第4回転から登場、ヨーロッパからやってきた謎の猫。どうやらシュレディンガー家から来たらしい。
母上：源次郎の母。文系だが、素粒子とスピンに興味がある。昆虫・植物が大好きで、KEK構内で撮った珍しい虫の写真を持ち歩く。
プロフィールはKEKのひと「山を旅して世界を知った 北村節子さん」に詳しい。 2020年8月まで、KEKの監事を務めた。
【KEKエッセイ #1】天才はおもいがけなくやってくる
【KEKエッセイ #7】メンデレーエフの日本の孫
【KEKエッセイ #15】原爆投下。チャーチルは、ママの実家を頼った？
【KEKエッセイ #24】偉大な博士の「最後のイチジクの葉」
【KEKエッセイ #31】「珈琲」「元素」を生んだ幕末のサラブレッド
前回までのお話：
前回のあらすじ：
わたスピ基礎編卒業を認定された母上と、猫の 源次郎、シュレ子の旅は続く。 母上の次の疑問は「陽子のスピンはどうやって発見されたか」なのだが、陽子のスピンにたどり着く前に水素分子が立ちはだかった。
さらにパウリの排他律に従わない粒子があると聞いて母上は絶句。
しかし、北村さんは大丈夫でしたかね。パウリの排他律に従わない粒子があるかもというのでびっくりされたんでしょうね。
とても熱心な方だからね。
大丈夫。きっと今日もまた元気に登場するよ。
それならいいんだけど…。
それよりも、今日はいよいよ波動関数の話をしなきゃならないよ。
そうだった。気を引き締めていきましょう。
じゃ、今日もよろしくお願いします。
今回の教科書
「スピンはめぐる 成熟期の量子力学」
著者：朝永 振一郎
1974年7月初版発行 中央公論社
2008年6月新版発行 みすず書房
担任：村上 洋一（むらかみ よういち）さん
愛媛県松山市出身。専門は、物性物理学。幼いころから磁石の不思議に魅せられて、かれこれ半世紀、磁石に関連した研究を続け、2021年3月までKEK 物構研の教授を務めた。退職後は新しいことを学ぶ時間ができた。
【KEKエッセイ #10】百万聞は一見に如かず～光を作る工場
【KEKエッセイ #19】相転移～景色が突然変わるとき
【KEKエッセイ #28】電子の不思議 ～遍歴と局在の狭間で～
【KEKエッセイ #37】協奏的な量子ビーム利用で物性発現機構を探る
千葉県松戸市出身の理論物理学者。2020年3月まで、KEK 素粒子物理学研究所 理論センターに所属、同年4月から長崎総合科学大学 教授。
高エネルギー重イオン衝突や高エネルギーのハドロン散乱などの極限的な状況の物理に興味を持って研究している。
板倉さん、こんにちは！ 今日も張り切ってますね。 前回、パウリの排他律に従わない粒子があるということをお聞きしました。 そうでしたか。では改めて説明しましょう。 なるほど、そうすると、電子はパウリの排他律に従うからフェルミ粒子、というわけね。 この話を始めると「量子統計力学」という分野に入ってしまうので、深入りはしないでおきたいんですが、 ボース粒子は1924年に確立されたいわゆる「ボース＝アインシュタイン統計」に従う粒子、フェルミ粒子は1926年に確立されたいわゆる「フェルミ＝ディラック統計」に従う粒子で、それぞれ違ったふるまいをします。 分かりました…。 実は陽子のスピンを調べることと、陽子がどちらに分類されるか、ということには深い関係があるんですよ。 陽子のスピン発見と、粒子としての分類の過程が分かるということなのね。 そうです。
初めまして、フントです。 どうも、初めまして。よろしくお願いします。 1927年には、電子がフェルミ粒子で、光子がボース粒子だということくらいしか分かっていませんでした。 じゃあ、陽子がどちらなのかを確かめたかったということですね？ はい。 そうですね。わたスピ4では波動関数の意味を考えていましたね。 じゃあ、粒子の交換と対称、反対称って？ 粒子を交換するということは粒子の場所を入れ替えるということです。 ふんふん。 粒子の座標が入れ替わったときに波動関数の符号が変わらなければ対称、符号が変わったら反対称、って呼ぶんです。 ふーん。 ピンとこないようだから、具体的に考えてみますか。 2つの粒子の交換なら、ちょっとイメージできるかも。 わたスピ4で、波動関数の二乗が粒子が存在する確率分布になるという話をしていましたね。陽子1が位置 x1に、陽子2が位置 x2にいる確率を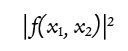
とします。f は function（関数）の f 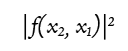です。
です。ふむふむ。 本来、陽子は区別できないので、陽子が位置を交換しても存在確率は変わらないはずです。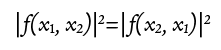
とすると、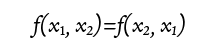
の場合と、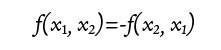
の場合が考えられる。ふむふむ。 もし陽子がボース粒子なら、2つの核を交換しても波動関数の符号は変わらない。 あ、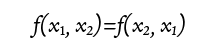
が、ボース粒子で、
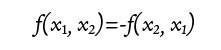が、フェルミ粒子！ そうなんですよ。パウリの排他律に従う粒子はひっくり返っちゃうんです。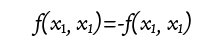
となりますね。これを満たすのは
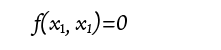になってしまうので、粒子の存在確率もゼロです。 な・る・ほ・ど！ 座標を取り換えたときに符号が変わらない関数を対称関数、変わる関数を反対称関数といいます。
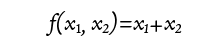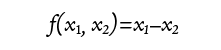かな。
かな。
それでは、本題に戻って水素分子のエネルギーと波動関数を考えてみましょう。 水素分子のエネルギーをその各運動状態のエネルギーの和で表していましたね。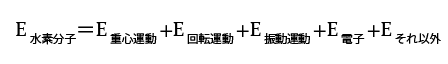
これが、波動関数ではかけ算になるんだ。
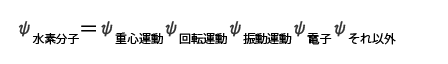となる。 え、どうして？ 私は、対称性だけを手がかりに、水素分子のエネルギーを考えてみたんだ。
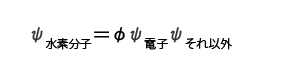
だいぶシンプルな式になったわ。 2つの同じ種類の原子核を交換しても重心は変わらないね？ はい。 交換しても変わらないということは、つまり、 振動は、2つの原子核の距離が問題になるんだけど、距離は原子核を交換しても変わらない。 確かに。 つまり、ψ振動運動もいつでも対称関数。それと、十分に低温だと振動のエネルギーはとても小さい。 なるほど。 そう。だから問題になるのが、回転運動なんだ。 そうですね。 一番小さいエネルギーを0番目、次を1番目、2番目…と数えて その0,1,2,…の記号を
J
としよう。
J
は0以上の整数ですよ。 なんと回転運動の式 ψ回転運動は へぇ。 そうそう。J=1では、φは対称関数と反対称関数と対称関数のかけ算だから、反対称関数になるね。 ここで、もし陽子がスピンを持たず、球対称な粒子だと仮定すると、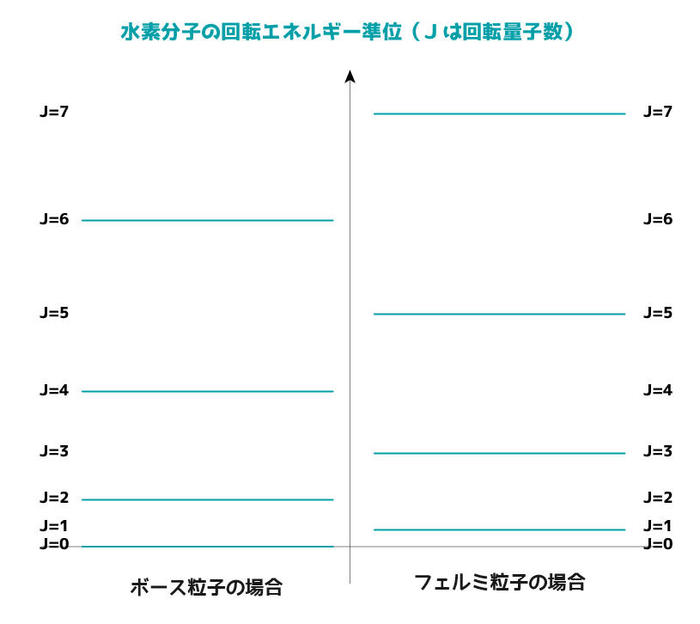
回転エネルギー準位がさらに飛び飛びになってる！ さぁ、ここで水素分子の波動関数はφである、と考えていいなら、あとは実験でどちらのグラフが正しいか調べればいいということになる。 えーっと、でもそうすると「それ以外のエネルギー」は無視されたまま？ それじゃ、陽子のスピンの話が終わっちゃうニャ～ 大丈夫、話はここからですから。 ひとひねりって？ それ以外のエネルギーが加わると、波動関数はこんなかけ算になるね。
え～っと、グラフがさっきみたいな一つおきではなくなるってことかしら。
はい。おそらくそうだろうと私は考えました。きれいに一つおきじゃないけど、一つおきの名残りは残って、一つおきに強い弱いがくると思ったんですよね。例えばこんな感じに…
それで「ひとひねり」ですか。 キーワードは縮退度ですね。 縮退度って？ 同じエネルギーの値を持っていても、全く同じ状態とは限らない。各エネルギーが幾つの状態から成っているか、その数を「縮退度」と言います。 はぁ。 同じエネルギーを持っていても異なる状態が2つあれば、縮退度は2と数えます。同様に、異なる状態が n 個あれば、縮退度は n です。 それで縮退度がどう関係するんですか？ 一般的に、エネルギーが同じでも中身が違う状態がいくつもあると、その状態の数がエネルギーの計算に必要になるんです。 ふうん。水素分子の場合は？ それ以外のエネルギーを表す波動関数ψそれ以外の対称性によって縮退度が違う可能性があると考えたんだよ。 縮退って縮こまるって字を使うけど、スペクトル強度が強くなるのね。 日本語では「縮重」と呼ぶこともありますよ。同じところに折り重なっているからスペクトル線が強くなるんだね。 それで、私がそれまでの実験結果と計算から立てた予測はこれです。線の太さで強度を表しています。
これがちゃんと計算した結果ね！ それから強度比を仮定して式を立て、自分の持っている比熱の実験データを使って水素分子の慣性モーメントを求めてみた。 あらまぁ。 私の仕事はここまでだ。 お疲れさまでした…。 あとは実験でそれぞれの準位のスペクトル強度が調べられれば… 結局、比熱の実験だけでは陽子のスピンを確かめられなかったけど、 日本人と聞くと急に親近感がわくわね。 えーっと、1899年だから、明治32年生まれだね。 そのときに彼らに量子力学の魅力を語り、刺激を与えたと言われていますよね。 じゃあ、堀 健夫との出会いがなければ、彼らのノーベル賞受賞もなかったかもしれないということかしら。 そうかもしれないね。1923年ころだから、欧米ではスピンの概念が生まれつつあるころ。和暦で言うと、大正12年ころだよ。 堀の生まれた時代には、世界の人口は16億人程度でしたが、そのうちアカデミックな物理学の研究者は全世界で1,500人程度だったと言われていますから、いまよりもずっと狭いコミュニティだったと思います。
当時はどういう実験をしたの？ そのころは、放電管の中に稀薄なガスを入れ、そこに電圧をかけることで放電を起こして生成した光のスペクトルを調べるという実験が盛んに行われていたそうです。 きょく紫外線？ 紫外線よりも高いエネルギーを持つ光のことだよ。フォトンファクトリーでも極紫外線を出しています。
堀は、水素分子の電子励起に関係するエネルギー準位構造を、水素分子から発せられる光の極紫外線領域を見ることによって調べたのですよ。 もちろん、水素分子の回転エネルギーを測るためには極低温での実験ということになりますね。 それで、堀の実験で何が分かったの？ 堀は、スペクトルの強度が 移るとき…？ 北村さん、わたスピ2を思い出そう。原子が光を出すのはどんなとき？ あ！ 飛び飛びのエネルギー間をジャンプするとき余ったエネルギーを出すんだった。 そうそう。 じゃ、続けますよ。 ということは？ この結果とフントが描いたグラフを見比べると、フェルミ粒子の場合に当てはまります。 右のグラフは J が奇数のとき太い。 フントさんの理論のうち、どちらが正しいか実験で確かめられたってことね。 さらに、アメリカからボーア研究所に来たデニソンが堀の水素分子実験のデータを見て、短い論文を書いています。
ふんふん、その2つの状態の違いは水素の原子核のスピンのせい、ってことかしら。 そうなんです。 この、常温でのオルソ水素とパラ水素の存在比が3：1というのは、いまでも使われるとても有名な値ですよ。 でもちょっと待って。堀は極低温で実験したんじゃなかった？ 常温なら、強度比と存在比は近似していいことが理論式から導けるんです。 まさにそこが、フントと堀の研究をまとめたデニソンの功績ってことなんだよね。 さらにそこから、陽子のスピンの大きさは電子のスピンの大きさと同じであることも導けた。 ふーん、スピンの大きさまで分かっていたんですか。さらっと説明されるということはまた数学が出てくるってことなのよね。ここは、飲み込むことにしましょう。 オルソ（ortho）とパラ（para）はギリシャ語で、それぞれ「正規の」「反対の」などという意味です。 なるほど～。 パラはパラリンピックのパラかと思ったニャ。 パラリンピックのパラは、脊髄損傷などで下半身が麻痺した人を指すパラプレジアから来てるのよ。 そのパラはパラライズド（麻痺した）からきていて、このパラはやはり「反対の」とか「脇に」という意味なんです。 じゃあ、やっぱり同じパラなんだにゃ～。 そういえば、ボーアはサッカーのデンマーク代表補欠としてオリンピックに出場したとかしないとか…。 ボーアは確かにサッカーが上手かったらしいですが、ボーアではなく、数学者になった弟ハラルトが1908年のロンドンオリンピック代表になって銀メダルを獲得したらしいですね。 へぇ、文武両道に長けた兄弟だったのねぇ。 オリンピックは参加することに意味があるにゃ～。 その言葉は現代ではほとんど死語になっちゃったニャ。 ところでところで、 比熱と分光実験だけで、陽子がスピンを持つと言えたの？確か前々回の終わりで村上先生がノーベル賞の話をしてたニャ。
それでは次回は決定打となった実験の話をしましょうか。おなじみのシュテルン・ゲルラッハ実験です。 楽しみにしてます。前回までのお話一覧：
スピンオフコラム：
